二叉树是一种重要的数据结构，在计算机科学和算法中广泛应用。对二叉树进行遍历是一种基本操作，其中包括前序遍历、中序遍历和后序遍历。本文将详细讲解这三种遍历算法的原理和实现方法。

二叉树的简介

二叉树是一种常见的树形数据结构，它由节点（Node）组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树的特点是每个节点最多有两个子节点，且子节点的位置是固定的，左子节点在父节点的左边，右子节点在父节点的右边。而在二叉树中满二叉树是一种特殊类型的二叉树，它的定义是：在满二叉树中，除了叶子节点外，每个节点都有两个子节点，并且所有叶子节点都在同一层级上。以下遍历算法均以这颗满二叉树为例。

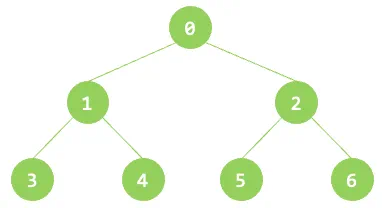
示例代码：

//定义树
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
}

前序遍历算法

前序遍历是一种深度优先的遍历方式，遍历顺序为根节点、左子树、右子树。具体步骤：判断树是否为空，是则返回，反之。访问当前节点。递归地对左子树进行前序遍历。递归地对右子树进行前序遍历。遍历顺序为：​0 -> 1 -> 3 -> 4 -> 2 -> 5 -> 6​。

前序遍历的代码实现：

public void postorderTraversal(TreeNode root) {
    if (root == null) return;

    System.out.print(root.val + " "); // 输出当前节点
    
    postorderTraversal(root.left); // 递归遍历左子树
    
    postorderTraversal(root.right); // 递归遍历右子树
}

中序遍历算法

中序遍历是一种深度优先的遍历方式，遍历顺序为左子树、根节点、右子树。具体步骤如下：判断树是否为空，是则返回，反之。递归地对左子树进行中序遍历。访问当前节点。递归地对右子树进行中序遍历。遍历顺序为：​3 -> 1 -> 4 -> 0 -> 5 -> 2 -> 6​。

中序遍历的代码实现：

public void inorderTraversal(TreeNode root) {
    if (root == null) return;
    
    inorderTraversal(root.left); // 递归遍历左子树
    
    System.out.print(root.val + " "); // 输出当前节点
    
    inorderTraversal(root.right); // 递归遍历右子树
}

后序遍历算法

后序遍历是一种深度优先的遍历方式，遍历顺序为左子树、右子树、根节点。具体步骤：判断树是否为空，是则返回，反之。递归地对左子树进行后序遍历。递归地对右子树进行后序遍历。访问当前节点。遍历顺序为：​3 -> 4 -> 1 -> 5 -> 6 -> 2 -> 0​。

后序遍历的代码实现：

public void postorderTraversal(TreeNode root) {
    if (root == null) return;
    
    postorderTraversal(root.left); // 递归遍历左子树
    
    postorderTraversal(root.right); // 递归遍历右子树
    
    System.out.print(root.val + " "); // 输出当前节点
}

总结

前序遍历、中序遍历和后序遍历是二叉树遍历中常用的三种算法。它们通过递归的方式按照不同的顺序遍历二叉树的节点。通过理解这些遍历算法的原理和代码实现，我们可以更好地操作和分析二叉树数据结构，在算法和应用中灵活应用它们。

如果你对编程知识和相关职业感兴趣，欢迎访问编程狮官网（https://www.w3cschool.cn/）。在编程狮，我们提供广泛的技术教程、文章和资源，帮助你在技术领域不断成长。无论你是刚刚起步还是已经拥有多年经验，我们都有适合你的内容，助你取得成功。