numpy之linspace()函数使用详解
linspace() 函数
作为序列生成器, numpy.linspace()函数用于在线性空间中以均匀步长生成数字序列。
Numpy通常可以使用numpy.arange()生成序列,但是当我们使用浮点参数时,可能会导致精度损失,这可能会导致不可预测的输出。为了避免由于浮点精度而造成的任何精度损失,numpy在numpy.linspace()为我们提供了一个单独的序列生成器,如果您已经知道所需的元素数,则这是首选。 但是通常使用带有适当参数的linspace()和
arange()可以得到相同的输出,因此可以为同一任务选择两者。
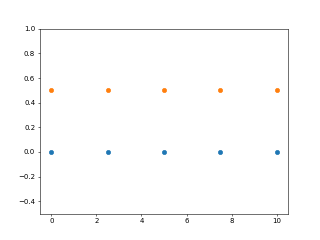
例如,以下代码使用numpy.linspace()在0到10之间绘制2个线性序列,以显示该序列生成的均匀性。
import numpy as np
import matplotlib.pyplot as plt
y = np.zeros(5)
x1 = np.linspace(0, 10, 5)
x2 = np.linspace(0, 10, 5)
plt.plot(x1, y, 'o')
plt.plot(x2, y + 0.5, 'o')
plt.ylim([-0.5, 1])
plt.show()
输出 :
语法:
格式: array = numpy.linspace(start, end, num=num_points)将在start和end之间生成一个统一的序列,共有num_points个元素。
- start -> Starting point (included) of the rangestart ->范围的起点(包括)
- end -> Endpoint (included) of the rangeend ->范围的端点(包括)
- num -> Total number of points in the sequencenum >序列中的总点数
让我们通过几个示例来理解这一点:
import numpy as np
a = np.linspace(0.02, 2, 10)
print('Linear Sequence from 0.02 to 2:', a)
print('Length:', len(a))
Linear Sequence from 0.02 to 2: [0.02 0.24 0.46 0.68 0.9 1.12 1.34 1.56 1.78 2. ]
Length: 10
上面的代码段生成了0.02到2之间的均匀序列,其中包含10个元素。
endpoint 关键字参数
如果您不想在序列计算中包括最后一点,则可以使用另一个关键字参数endpoint ,可以将其设置为False 。 (默认为True )
import numpy as np
a = np.linspace(0.02, 2, 10, endpoint=False)
print('Linear Sequence from 0.02 to 2:', a)
print('Length:', len(a))
Linear Sequence from 0.02 to 2: [0.02 0.218 0.416 0.614 0.812 1.01 1.208 1.406 1.604 1.802]
Length: 10
如您所见,最后一点(2)没有包含在序列中,因此步长也不同,这将产生一个完全不同的序列。
retstep 关键字参数
这是一个布尔型可选参数(如果已指定),还将返回步长以及序列数组,从而产生一个元组作为输出
import numpy as np
a = np.linspace(0.02, 2, 10, retstep=True)
print('Linear Sequence from 0.02 to 2:', a)
print('Length:', len(a))
输出
Linear Sequence from 0.02 to 2: (array([0.02, 0.24, 0.46, 0.68, 0.9 , 1.12, 1.34, 1.56, 1.78, 2. ]), 0.22)
Length: 2
由于输出是元组,因此它的长度是2,而不是10!
axis 关键字参数
这将在结果中设置轴以存储样本。 仅当开始和端点为数组数据类型时才使用它。
默认情况下( axis=0 ),采样将沿着在开始处插入的新轴进行。 我们可以使用axis=-1来获得末端的轴。
import numpy as np
p = np.array([[1, 2], [3, 4]])
q = np.array([[5, 6], [7, 8]])
r = np.linspace(p, q, 3, axis=0)
print(r)
s = np.linspace(p, q, 3, axis=1)
print(s)
输出
array([[[1., 2.],
[3., 4.]],
[[3., 4.],
[5., 6.]],
[[5., 6.],
[7., 8.]]])
array([[[1., 2.],
[3., 4.],
[5., 6.]],
[[3., 4.],
[5., 6.],
[7., 8.]]])
在第一种情况下,由于axis = 0 ,我们从第一个轴获取序列限制。
在这里,限制是子数组对[1, 2] and [5,6]以及[3, 4] and [7,8] ,它们取自p和q的第一轴。 现在,我们比较结果对中的相应元素以生成序列。
因此,第一行的顺序为[[1 to 5], [2 to 6]] ,第二行的顺序为[[1 to 5], [2 to 6]] [[3 to 7], [4 to 8]] ,对其进行评估并组合形成[ [[1, 2], [3, 4]], [[3, 4], [5, 6]], [[5, 6], [7,8]] ] 。
第二种情况将在axis=1或列中插入新元素。 因此,新轴将通过列序列生成。 而不是行序列。
考虑序列[1, 2] to [5, 7]和[3, 4] to [7, 8]并将其插入到结果的列中,得到[[[1, 2], [3, 4], [5, 6]], [[3, 4], [5, 6], [7, 8]]] 。
推荐好课:Python3进阶:数据分析及可视化、Python 自动化办公