在之前我们对html5canvas这个属性讲解了很多有关于这方么的实现方法，那么今天我们来讲讲有关于：“在html5中使用Canvas完成文本填充线性渐变的使用和方法解析！”这方面的相关内容！

前言

在 Canvas 中对文本填充水平或垂直的线性渐变可以轻易实现，而带角度的渐变就复杂很多；就好像下面这样，假设文本矩形宽为 W, 高为 H, 左上角坐标为 X, Y。

猜想与答案

给出两个答案：

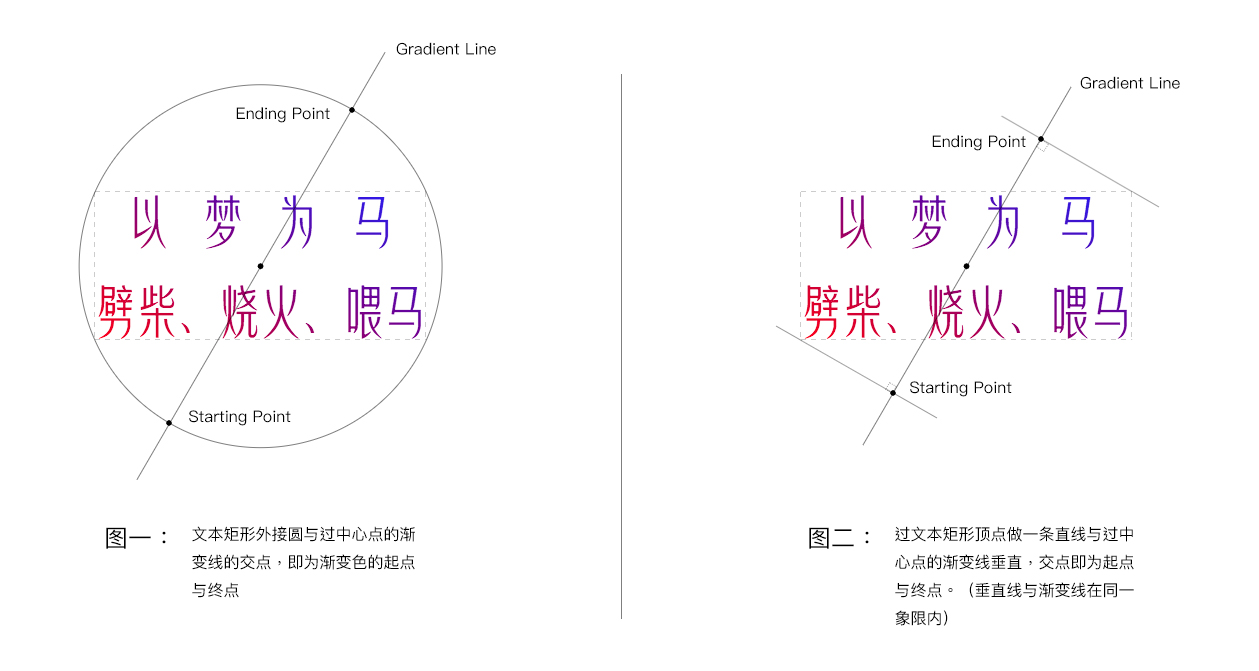
正确答案是图二，因为这样得出来的坐标生成的渐变最紧接文本矩形边界，它的运动轨迹如下动图：

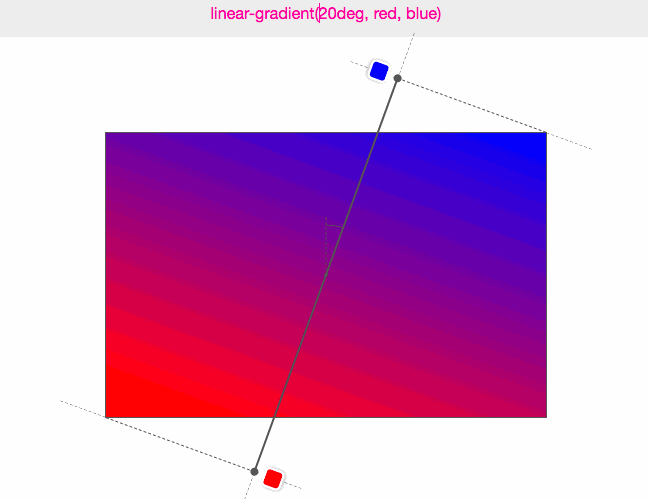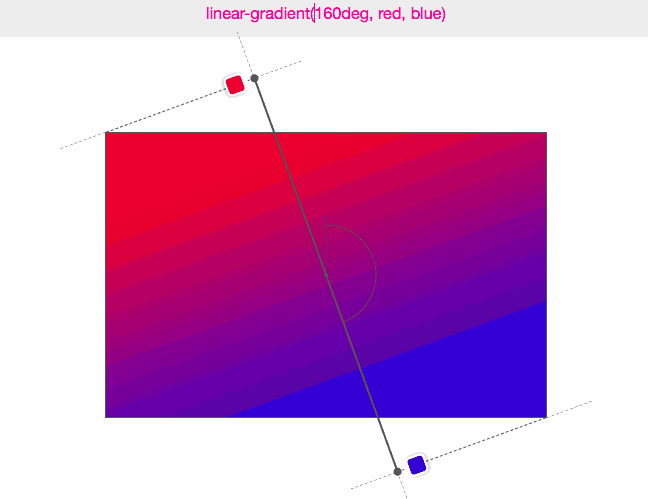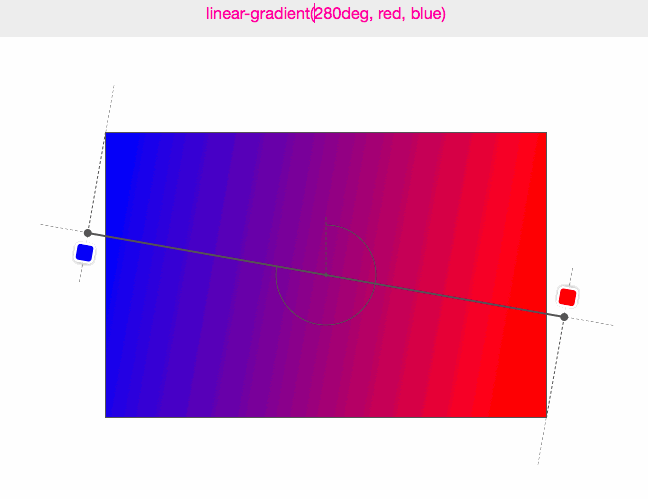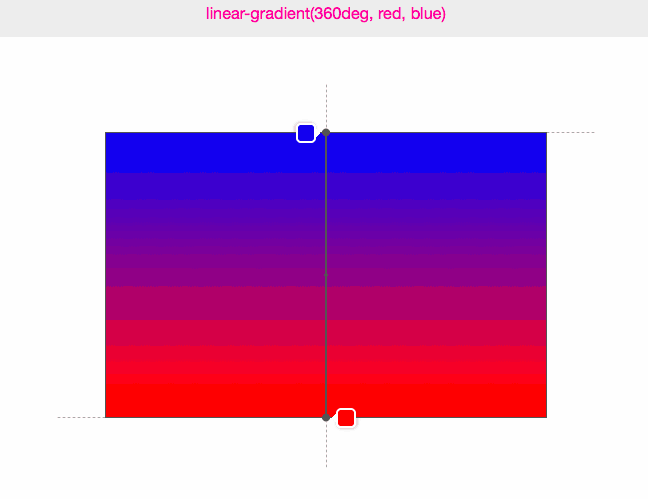
(图来源：Do you really know CSS linear-gradients）

渐变起点与终点坐标的计算

所以，渐变的起点与终点坐标该怎么计算呢？答:

1. 先求得起点与终点的长度（距离）。
2. 根据长度与文本矩形的中心点坐标分别计算出起点与终点坐标。

线性渐变长度的计算 W3C 给出了一个公式（A 表示角度）：

gradientLineLength = abs(W * sin(A)) + abs(H * cos(A))

不过，该公式主要应用于 CSS 的线性渐变设置，即以 12 点钟方向为 0°，顺时针旋转。

而我们需要的是以 3 点钟方向为 0°，逆时针旋转，即公式为：

gradientLineLength = abs(W * cos(A)) + abs(H * sin(A))

// 半长：
halfGradientLineLength = (abs(W * cos(A)) + abs(H * sin(A))) / 2

那么这个公式是怎么来的呢？以下是笔者的求解：

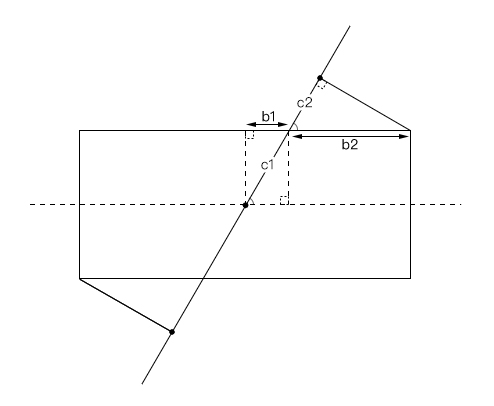
由图可得以下方程组：

因此可推导出：

化简后为：

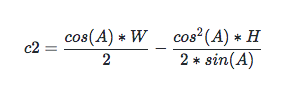
所以 c1 + c2 为：

由三角函数平方公式知：cos(A) * cos(A) = 1 - sin(A) * sin(A)， 代入 c1 + c2：

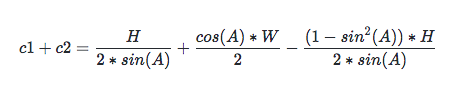
第一步化简后：

最后的结果就是：

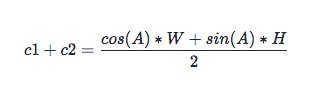
因为 sin, cos 在函数周期内存在负值（见下面角度对应的三角函数周期图），所以线性渐变的长度需要取绝对值。

至此，我们知道了线性渐变长度，文本矩形的中心点坐标很好算，即：

centerX = X + W / 2
centerY = Y + H / 2

所以，起点与终点的坐标分别为：

startX = centerX - cos(A) * halfGradientLineLength
startY = centerY + sin(A) * halfGradientLineLength

endX = centerX + cos(A) * halfGradientLineLength
endY = centerY - sin(A) * halfGradientLineLength

看看最终效果

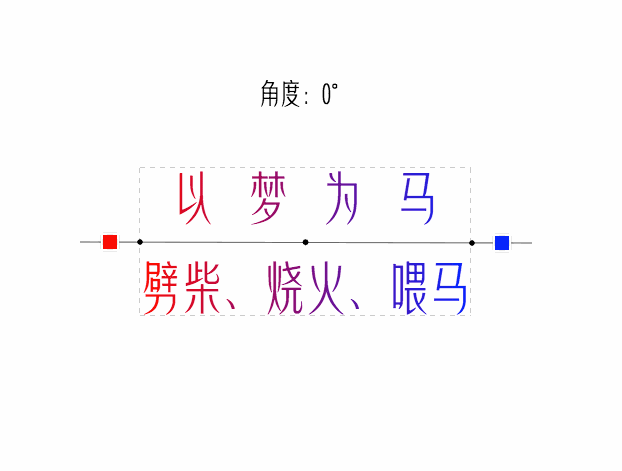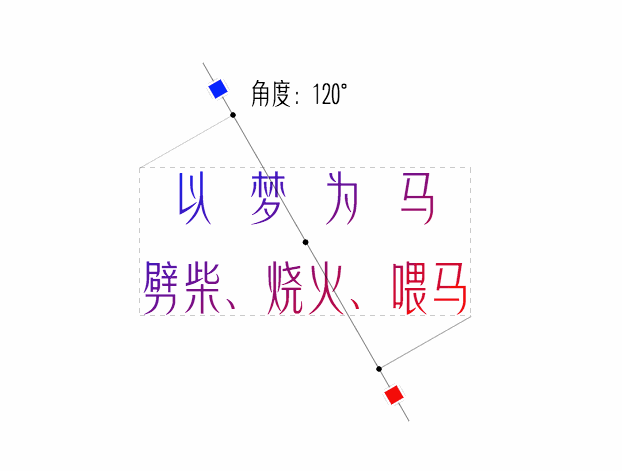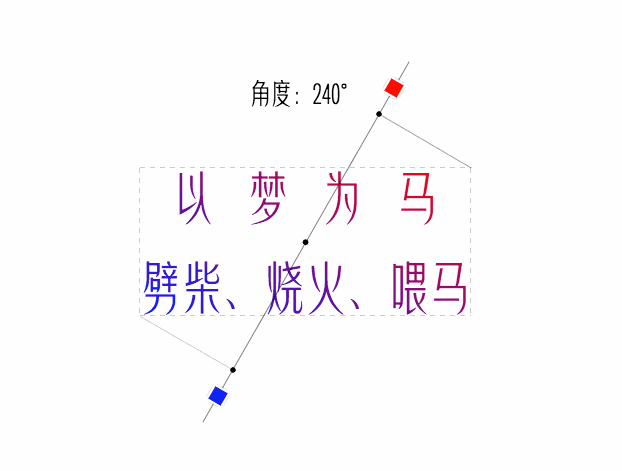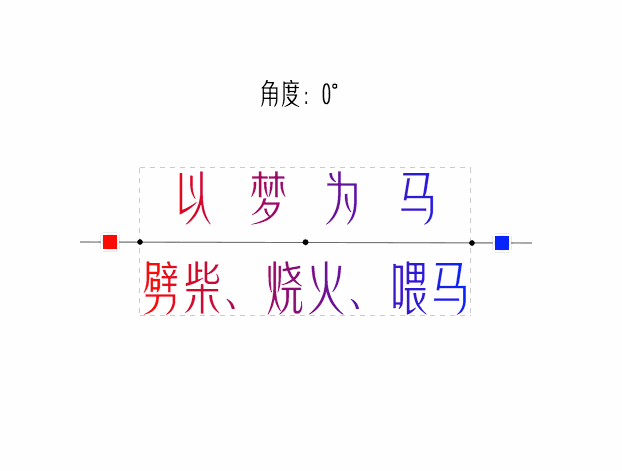
经验注释

进行三角函数计算时，应尽量避免先用 tan, 因为 tan 在其周期内存在无穷值，需要做特定的条件判断，而 sin, cos 没有此类问题，代码书写更为简洁清晰并且不会因疏忽产生错误，见下面三角函数与角度的对应关系周期图。

参阅

Do you really know CSS linear-gradients?

MDN linear-gradient

W3C - CSS Images Module Level 3 # linear-gradients

那么我们今天有关于：“在html5中使用Canvas完成文本填充线性渐变的使用和方法解析！”这个方面的内容就到此了，更多有关于html5canva这方面的使用我们都可以在W3Cschool中进行学习和了解！