异常值是数据集的重要组成部分。它们可以保存有关您数据的有用信息。异常值可以为您正在研究的数据提供有用的见解，并且它们可以对统计结果产生影响。这可能会帮助您发现不一致之处并检测统计过程中的任何错误。因此，了解如何在数据集中查找异常值将有助于您更好地理解数据。

有几种不同的方法可以在统计中找到异常值。本文将解释如何通过计算四分位距来检测数值异常值。我举了一个非常简单的数据集以及如何计算四分位距的示例，因此您可以根据需要进行操作。让我们开始吧！

什么是统计中的异常值？

简单来说，异常值是相对于最近的数据点和您正在使用的数据图或数据集中的其余相邻共存值而言极高或极低的数据点。

离群值是从数据集或图形中的整体值模式中显着突出的极值。

下面，在图表的最左侧，有一个异常值。

一月份的值明显低于其他月份。

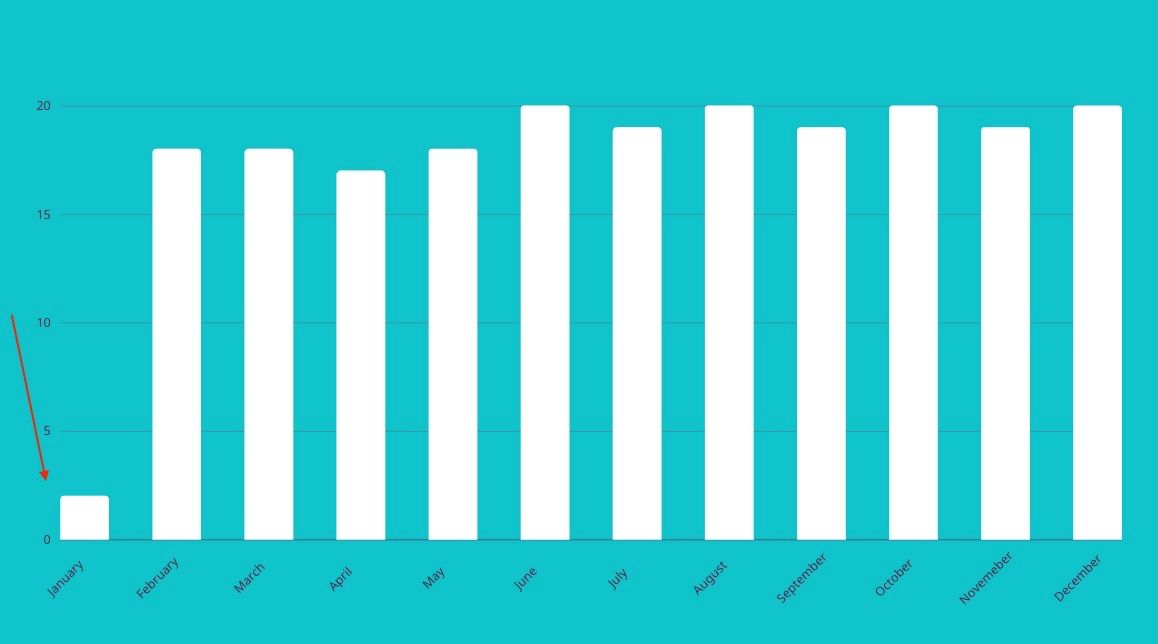
如何识别数据集中的异常值

好的，你如何寻找异常值？

异常值必须满足以下两个条件之一：

outlier < Q1 - 1.5(IQR)

outlier > Q3 + 1.5(IQR)

低离群值的规则是数据集中的数据点必须小于​Q1 - 1.5xIQR​。

这意味着数据点需要低于第一个四分位数的四分位间距的 1.5 倍以上才能被视为低异常值。

高离群值的规则是，如果数据集中的任何数据点大于​Q3 - 1.5xIQR​，则为高离群值。

更具体地说，数据点需要落在第三个四分位数以上的四分位距的 1.5 倍以上才能被视为高异常值。

如您所见，您需要首先在数据集中计算某些个别值，例如IQR. 但是要找到IQR，您需要找到分别是Q1和 的所谓的第一四分位数和第三四分位数 Q3。

所以，让我们看看它们各自做了什么，并分解如何在奇数和偶数数据集中找到它们的值。

如何在奇数数据集中找到上下四分位数

首先，假设您有这个数据集：

25,14,6,5,5,30,11,11,13,4,2

第一步是按数字升序对值进行排序，从最小到最大。

2,4,5,5,6,11,11,13,14,25,30

最低值 ( MIN ) 是2，最高值 ( MAX ) 是30。

如何在奇数数据集中计算Q2

下一步是找到中位数或四分位数 2 (Q2)。

这组特定的数据具有奇数个值，11总分加在一起。

在数据集中查找中位数意味着您正在查找中间值——集合中的单个中间数。

在奇数数据集中，只有一个中间数。

因为11总共有值，所以一个简单的方法是将集合分成两个相等的部分，每边包含5值。

中值将5在一侧具有值，在另一侧具有值5。

(2,4,5,5,6), 11,(11,13,14,25,30)

中位数是11因为它是将前半部分与后半部分分开的数字。

仔细检查您是否正确的另一种方法是这样做：

(total_number_of_scores + 1) / 2.

这是(11 + 1) /2 = 6，这意味着您希望在6th这组数据的位置使用数字 - 即11。

所以Q2 = 11。

如何在奇数数据集中计算Q1

接下来，为了找到下四分位数，Q1我们需要找到数据集前半部分的中位数，它位于左侧。

提醒一下，初始数据集是：

(2,4,5,5,6), 11,(11,13,14,25,30)

数据集的前半部分或下半部分不包括中位数：

2,4,5,5,6

这一次，又是一组奇怪的分数——特别是有5值。

您想再次将这半集分成另一半，每侧有相同数量的两个值。您将获得一个唯一编号，该编号将是5值中间的编号。

选择突出的中间值：

(2,4), 5,(5,6)

在这种情况下，它是Q1 = 5.

要仔细检查，您还可以执行total_number_of_values + 1 / 2类似于前面的示例：

(5 + 1) /2 = 3.

这意味着您需要第三位的数字，即5.

如何在奇数数据集中计算Q3

要找到上四分位数Q3，过程与Q1上述相同。但在这种情况下，你在数据集的右侧取下半部分，高于中位数，不包括中位数本身：

(2,4,5,5,6), 11,(11,13,14,25,30)

11,13,14,25,30

您将奇数集的这一半拆分为另一半以求中位数，然后求出 的值Q3。

您再次希望像上半场一样排在第三位。

(11,13), 14,(25,30)

所以Q3 = 14。

如何在奇数数据集中计算IQR

现在，下一步是计算代表四分位距的 IQR。

这是您在上面计算的下四分位数 (Q1) 和上四分位数 (Q3) 之间的差异/距离。

提醒一下，这样做的公式如下：

IQR = Q3 - Q1

要从上面找到数据集的 IQR：

IQR= 14 - 5
IQR = 9

如何在奇数数据集中找到异常值

回顾到目前为止，数据集如下：

2,4,5,5,6,11,11,13,14,25,30

到目前为止，您已经计算了五个数字摘要：

MIN = 2
Q1 = 5
MED = 11
Q3 = 14
MAX = 30

最后，让我们看看数据集中是否有任何异常值。

提醒一下，异常值必须符合以下标准：

outlier < Q1 - 1.5(IQR)

或者

outlier > Q3 + 1.5(IQR)

要查看是否有最低值异常值，需要计算第一部分，看看集合中是否有满足条件的数字。

Outlier < Q1 - 1.5(IQR)
Outlier < 5 - 1.5(9)
Outlier < 5 - 13.5 
outlier < - 8.5

没有更低的异常值，因为没有比-8.5数据集中的数字少的数字。

接下来，查看是否有更高的异常值：

Outlier > Q3  + 1.5(IQR)=
Outlier > 14 + 1.5(9)
Outlier > 14 + 13.5
Outlier > 27,5

并且数据集中有一个数字大于27,5：

2,4,5,5,6,11,11,13,14,25,30

在这种情况下，30是现有数据集中的异常值。

如何在偶数数据集中找到上下四分位数

当您的数据集由一组偶数数据组成时会发生什么？

不仅有一个突出的中位数 (Q2)，也没有突出的上四分位数 (Q1) 或突出的下四分位数 (Q3)。

所以计算四分位数然后找到异常值的过程有点不同。

如何在偶数数据集中计算Q2

假设你有这个带有8数字的数据集：

10,15,20,26,28,30,35,40

这一次，数字已经从最低值到最高值排序。

要在偶数数据集中找到中位数，您需要找到位于中间的两个数字之间的值。您将它们加在一起并除以2，如下所示：

10,15,20, 26,28,30,35,40

26 + 28 = 54
54 / 2 = 27

如何在偶数数据集中计算Q1

要计算偶数数据集中的上四分位数和下四分位数，您需要保留数据集中的所有数字（而不是在您删除中位数的奇数集中）。

这一次，数据集被切成两半。

10,15,20,26 | 28,30,35,40

为了 find Q1，您将数据集的前半部分拆分为另一半，留下剩余的偶数集：

10,15 | 20,26

要找到这一半的中位数，您可以将中间的两个数字除以二：

Q1 = (15 + 20)/2
Q1 =  35 / 2
Q1 = 17,5

如何在偶数数据集中计算Q3

要找到Q3，您需要关注数据集的后半部分并将该半部分拆分为另一半：

28,30,35,40 -> 28,30 | 35,40

中间的两个数字是30和35。

您将它们相加并将它们除以二，结果是：

Q3 = (30 + 35)/2
Q3 =  65 / 2
Q3 = 32,5

如何计算偶数数据集中的IQR

计算 IQR 的公式与我们用于计算奇数数据集的公式完全相同。

IQR = Q3 - Q1
IQR = 32,5 - 17,5
IQR = 15

如何在偶数数据集中找到异常值

回顾一下，到目前为止，五个数字摘要如下：

MIN = 10
Q1 = 17,5
MED = 27
Q3 = 32,5
MAX = 40

要计算数据集中的任何异常值：

outlier < Q1 - 1.5(IQR)

或者

outlier > Q3 + 1.5(IQR)

要找到任何较低的异常值，您可以计算Q1 - 1.5(IQR)并查看是否有任何值小于结果。

outlier < 17,5 - 1.5(15)=
outlier < 17,5 - 22,5
outlier < -5

数据集中没有任何小于 的值-5。

最后，为了找到任何更高的异常值，您计算 Q3 - 1.5(IQR)并查看数据集中是否有任何值高于结果

outlier > 32.5 + 1.5(15)=
outlier > 32.5 + 22.5
outlier > 55

没有任何高于55此数据集的值，因此该数据集没有任何异常值。

结论

在本文中，您学习了如何在数据集中查找四分位距并以此方式计算任何异常值。