Python机器学习之KNN近邻算法
在python机器学习中,KNN近邻算法是相当出名的存在。通过测量不同特征值之间的距离方法来进行分类,使它拥有了精度高,对异常值不敏感的优秀特点。那么这么出名的算法究竟是如何实现的呢?今天我们就从源代码来分析一下KNN近邻算法的实现。
一、KNN概述
简单来说,K-近邻算法采用测量不同特征值之间的距离方法进行分类
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高
适用数据范围:数值型和标称2型
工作原理:存在一个样本数据集合,也称为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系(训练集)。输入没有标签的新数据之后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签(测试集)。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处。(通常k不大于20)
二、使用Python导入数据
我们先写入一段代码
from numpy import * # 导入numpy模块
import operator # 导入operator模块
def createDataSet(): # 创建数据集函数
# 构建一个数组存放特征值
group = array(
[[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]
)
# 构建一个数组存放目标值
labels = ['A', 'A', 'B', 'B']
return group, labels
此处稍微介绍一下numpy这个包吧
三、numpy.array()
NumPy的主要对象是同种元素的多维数组。这是一个所有的元素都是一种类型、通过一个正整数元组索引的元素表格(通常是元素是数字)。
在NumPy中维度(dimensions)叫做轴(axes),轴的个数叫做秩(rank,但是和线性代数中的秩不是一样的,在用python求线代中的秩中,我们用numpy包中的linalg.matrix_rank方法计算矩阵的秩
线性代数中秩的定义:设在矩阵A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在的话)全等于0,那末D称为矩阵A的最高阶非零子式,数r称为矩阵A的秩,记作R(A)。
四、实施KNN分类算法
依照KNN算法,我们依次来
先准备好四个需要的数据
- inX:用于分类的输入向量inX
- dataSet:输入的训练样本集dataSet
- labels:标签向量labels(元素数目和矩阵dataSet的行数相同)
- k:选择最近邻居的数目
五、计算已知类别数据集中的点与当前点之间的距离
使用欧式距离:
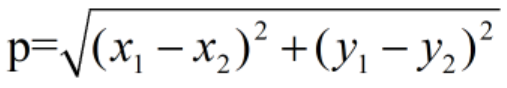
六、完整代码
# 返回矩阵的行数
dataSetSize = dataSet.shape[0]
# 列数不变,行数变成dataSetSize列
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
第一行
# 返回矩阵的行数
dataSetSize = dataSet.shape[0]
# 以第一步的数据为例
answer:4 # 4行第二行
inX = [1. , 0.]
# 列数不变,行数变成dataSetSize列
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
# tile(inX, (dataSetSize, 1))
inX = [
[1. , 0.],
[1. , 0.],
[1. , 0.],
[1. , 0.]
]
# inX - dataSet两个矩阵相减(行列相等相加相减才有意义)
dataSet = [
[1. , 1.1],
[1. , 1. ],
[0. , 0. ],
[0. , 0.1]
]
diffMat = [
[0. , -1.1],
[0. , -1.],
[1. , 0.],
[1. , -0.1]
]
第三行
# 求平方差
sqDiffMat = diffMat * 2第四行
# 计算矩阵中每一行元素之和
# 此时会形成一个多行1列的矩阵
sqDistances = sqDiffMat.sum(axis=1)第五行
# 开根号
distances = sqDistances**0.5按照距离递增次序排序
# 对数组进行排序
sortedDistIndicies = distances.argsort()选择与当前点距离最小的k个点
classCount = {} # 新建一个字典
# 确定前k个距离最小元素所在的主要分类
for i in range(k):
# voteIlabel的取值是labels中sortedDistIndicies[i]的位置
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
确定前k个点所在类别的出现概率
# 排序
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)###11# 返回前k个点出现频率最高的类别作为当前点的预测分类
return sortedClassCount[0][0]刚刚试一试C++的版本…小心,救命
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <map>
int sum_vector(std::vector<int>& v) {
int sum = 0;
for (int i = 0; i < v.size(); ++i) {
sum = v[i] + sum;
}
return sum;
}
int knn(int k) {
using std::cout;
using std::endl;
using std::vector;
vector<vector<int>> x;
vector<int> x_sample = {2, 3, 4};
for (int i = 0; i < 4; ++i) {
x.push_back(x_sample);
}
vector<int> y = {1, 1, 1, 1};
int dataSetSize = x.size();
vector<int> x_test = {4, 3, 4};
vector<vector<int>> x_test_matrix;
for (int i = 0; i < dataSetSize; ++i) {
x_test_matrix.push_back(x_test);
}
vector<int> v_total;
for (int i = 0; i < dataSetSize; ++i) {
for (int j = 0; j < x_test_matrix[i].size(); ++j) {
x_test_matrix[i][j] = x_test_matrix[i][j] - x[i][j];
x_test_matrix[i][j] = x_test_matrix[i][j] * 2;
}
int sum_vec = sum_vector(x_test_matrix[i]);
v_total.push_back(sqrt(sum_vec));
}
sort(v_total.begin(), v_total.end());
std::map<int, int> mp;
for (int i = 0; i < k; ++i) {
int label = y[v_total[i]];
mp[label] += 1;
}
int max_end_result = 0;
for (std::map<int, int>::iterator it = mp.begin(); it != mp.end(); it++) {
if (it->first > max_end_result) {
max_end_result = it->first;
}
}
return max_end_result;
}
int main() {
int k = 12;
int value = knn(k);
std::cout << "result:
" << std::endl;
return 0;
}
七、数据处理、分析、测试
处理excel和txt数据
excel数据是矩阵数据,可直接使用,在此不做处理。
文本txt数据需要一些数据处理
def file2matrix(filename):
fr = open(filename)
# 读取行数据直到尾部
arrayOLines = fr.readlines()
# 获取行数
numberOfLines = len(arrayOLines)
# 创建返回shape为(numberOfLines, 3)numpy矩阵
returnMat = zeros((numberOfLines, 3))
classLabelVector = []
index = 0
for line in arrayOLines:
# 去除首尾的回车符
line = line.strip()
# 以tab字符' '为符号进行分割字符串
listFromLine = line.split(' ')
# 选取前3个元素,把他们存储到特征矩阵中
returnMat[index, :] = listFromLine[0: 3]
# 把目标变量放到目标数组中
classLabelVector.append(int(listFromLine[-1]))
index += 1
return returnMat, classLabelVector
数据归一化和标准化
在数值当中,会有一些数据大小参差不齐,严重影响数据的真实性,因此,对数据进行归一化和标准化是使得数据取值在一定的区间,具有更好的拟合度。
例如归一化就是将数据取值范围处理为0到1或者-1到1之间
# max:最大特征值
# min:最小特征值
newValue = (oldValue - min)/(max-min)写个函数
def autoNorm(dataSet):
# min(0)返回该矩阵中每一列的最小值
minVals = dataSet.min(0)
# max(0)返回该矩阵中每一列的最大值
maxVals = dataSet.max(0)
# 求出极值
ranges = maxVals - minVals
# 创建一个相同行列的0矩阵
normDataSet = zeros(shape(dataSet))
# 得到行数
m = dataSet.shape[0]
# 得到一个原矩阵减去m倍行1倍列的minVals
normDataSet = dataSet - tile(minVlas, (m,1))
# 特征值相除
normDataSet = normDataSet/tile(ranges, (m, 1))
return normDataSet, ranges, minVals
归一化的缺点:如果异常值就是最大值或者最小值,那么归一化也就没有了保证(稳定性较差,只适合传统精确小数据场景)
标准化可查
八、鸢尾花数据测试
既然已经了解其内置的算法了,那么便调库来写一个吧
from sklearn.datasets import load_iris # 导入内置数据集
from sklearn.model_selection import train_test_split # 提供数据集分类方法
from sklearn.preprocessing import StandardScaler # 标准化
from sklearn.neighbors import KNeighborsClassifier # KNN
def knn_iris():
# 获得鸢尾花数据集
iris = load_iris()
# 获取数据集
# random_state为随机数种子,一个数据集中相等的行不能大于6
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)
# 特征工程:标准化
transfer = StandardScaler()
# 训练集标准化
x_train = transfer.fit_transform(x_train)
# 测试集标准化
x_test = transfer.transform(x_test)
# 设置近邻个数
estimator = KNeighborsClassifier(n_neighbors=3)
# 训练集测试形成模型
estimator.fit(x_train, y_train)
# 模型预估
# 根据预测特征值得出预测目标值
y_predict = estimator.predict(x_test)
print("y_predict:
", y_predict)
# 得出预测目标值和真实目标值之间是否相等
print("直接比对真实值和预测值:
", y_test == y_predict)
# 计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:
", score)
def main():
knn_iris()
if __name__ == '__main__':
main()
九、RESULT

到此这篇Python机器学习之KNN近邻算法的文章就介绍到这了,更多机器学习的内容请搜索W3Cschool以前的文章或继续浏览下面的相关文章。