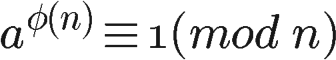欧拉函数的用处，在于[欧拉定理]。"欧拉定理"指的是：

如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

欧拉定理的证明比较复杂，这里就省略了。我们只要记住它的结论就行了。

欧拉定理可以大大简化某些运算。比如，7和10互质，根据欧拉定理，

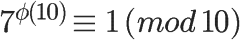
已知 φ(10) 等于4，所以马上得到7的4倍数次方的个位数肯定是1。

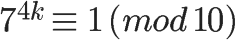
因此，7的任意次方的个位数（例如7的222次方），心算就可以算出来。

欧拉定理有一个特殊情况。

假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成

这就是著名的费马小定理。它是欧拉定理的特例。

欧拉定理是RSA算法的核心。理解了这个定理，就可以理解RSA。