Tensorflow.js 拟合曲线

这篇文章中，我们将使用TensorFlow.js来根据数据拟合曲线。即使用多项式产生数据然后再改变其中某些数据（点），然后我们会训练模型来找到用于产生这些数据的多项式的系数。简单的说，就是给一些在二维坐标中的散点图，然后我们建立一个系数未知的多项式，通过TensorFlow.js来训练模型，最终找到这些未知的系数，让这个多项式和散点图拟合。

先决条件

本教程假定您熟悉核心概念中介绍的TensorFlow.js的基本构建块：张量，变量和操作。我们建议在完成本教程之前先完成核心概念的学习。

运行代码

这篇文章关注的是创建模型以及学习模型的系数，完整的代码在这里可以找到。为了在本地运行，如下所示：

$ git clone https://github.com/tensorflow/tfjs-examples
$ cd tfjs-examples/polynomial-regression-core
$ yarn
$ yarn watch

即首先将核心代码下载到本地，然后进入polynomial-regression-core（即多项式回归核心）部分，最后进行yarn安装并运行。

输入数据

我们的数据集由x坐标和y坐标组成，当绘制在笛卡尔平面上时，其坐标如下所示：

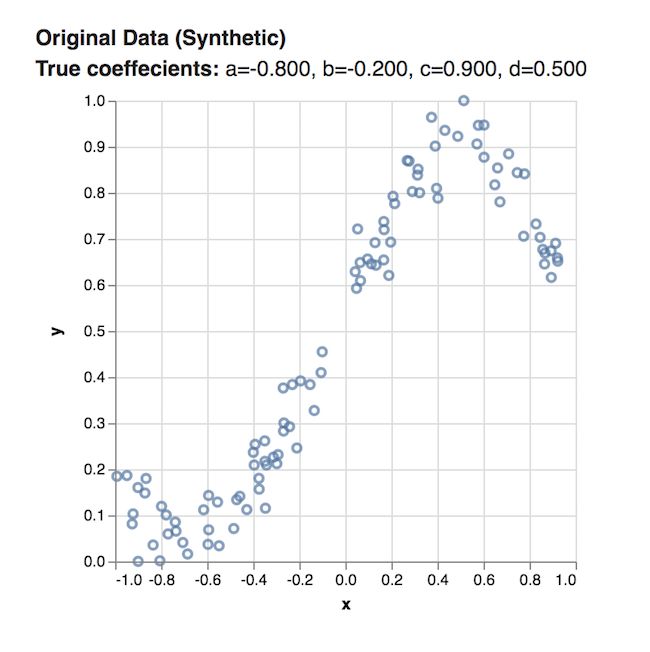
该数据是由三次方程 $y = ax^{3}+ bx^{2} + cx + d$ 生成的。

我们的任务是学习这个函数的a，b，c和d系数以最好地拟合数据。我们来看看如何使用TensorFlow.js操作来学习这些值。

学习步骤

第1步：设置变量

首先，我们需要创建一些变量。即开始我们是不知道a、b、c、d的值的，所以先给他们一个随机数，如下所示：

const a = tf.variable(tf.scalar(Math.random()));
const b = tf.variable(tf.scalar(Math.random()));
const c = tf.variable(tf.scalar(Math.random()));
const d = tf.variable(tf.scalar(Math.random()));

第2步：建立模型

我们可以通过TensorFlow.js中的链式调用操作来实现这个多项式方程 y = ax³ + bx² + cx + d，下面的代码就创建了一个 predict 函数，这个函数将x作为输入，y作为输出：

function predict(x) {
  // y = a * x ^ 3 + b * x ^ 2 + c * x + d
  return tf.tidy(() => {
    return a.mul(x.pow(tf.scalar(3))) // a * x^3
      .add(b.mul(x.square())) // + b * x ^ 2
      .add(c.mul(x)) // + c * x
      .add(d); // + d
  });
}

其中，在上一篇文章中，我们讲到tf.tify函数用来清除中间张量，其他的都很好理解。

接着，让我们把这个多项式函数的系数使用之前得到的随机数，可以看到，得到的图应该是这样：

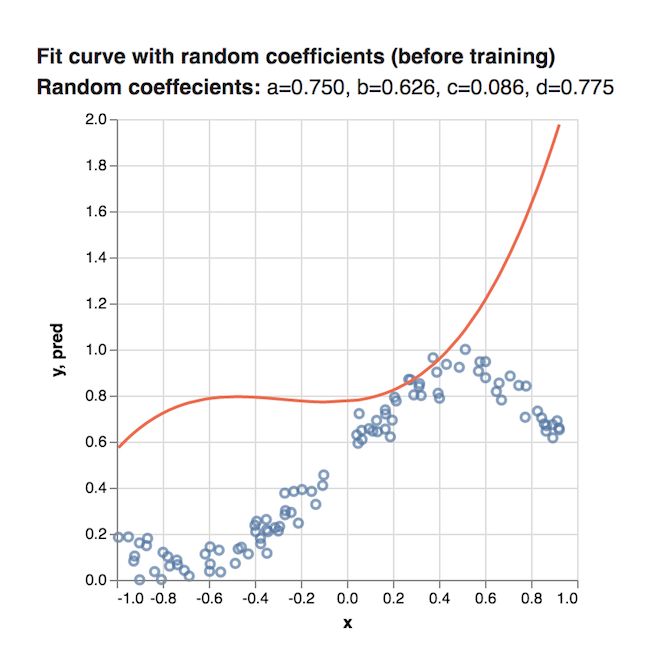
因为开始时，我们使用的系数是随机数，所以这个函数和给定的数据匹配的非常差，而我们写的模型就是为了通过学习得到更精确的系数值。

第3步：训练模型

最后一步就是要训练这个模型使得系数和这些散点更加匹配，而为了训练模型，我们需要定义下面的三样东西：

损失函数（loss function）：这个损失函数代表了给定多项式和数据的匹配程度。损失函数值越小，那么这个多项式和数据就跟匹配。
优化器（optimizer）：这个优化器实现了一个算法，它会基于损失函数的输出来修正系数值。所以优化器的目的就是尽可能的减小损失函数的值。
训练迭代器（traing loop）：即它会不断地运行这个优化器来减少损失函数。

所以，上面这三样东西的关系就非常清楚了：训练迭代器使得优化器不断运行，使得损失函数的值不断减小，以达到多项式和数据尽可能匹配的目的。这样，最终我们就可以得到a、b、c、d较为精确的值了。

定义损失函数

这篇文章中，我们使用MSE（均方误差，mean squared error）作为我们的损失函数。MSE的计算非常简单，就是先根据给定的x得到实际的y值与预测得到的y值之差的平方，然后在对这些差的平方求平均数即可。

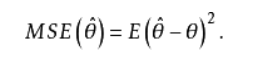
1044137-20180415120225981-2029551102

于是，我们可以这样定义MSE损失函数：

function loss(predictions, labels) {
  // 将labels（实际的值）进行抽象
  // 然后获取平均数.
  const meanSquareError = predictions.sub(labels).square().mean();
  return meanSquareError;
}

即这个损失函数返回的就是一个均方差，如果这个损失函数的值越小，显然数据和系数就拟合的越好。

定义优化器

对于我们的优化器而言，我们选用 SGD （Stochastic Gradient Descent）优化器，即随机梯度下降。SGD的工作原理就是利用数据中任意的点的梯度以及使用它们的值来决定增加或者减少我们模型中系数的值。

TensorFlow.js提供了一个很方便的函数用来实现SGD，所以你不需要担心自己不会这些特别复杂的数学运算。即 tf.train.sdg 将一个学习率（learning rate）作为输入，然后返回一个SGDOptimizer对象，它与优化损失函数的值是有关的。

在提高它的预测能力时，学习率（learning rate）会控制模型调整幅度将会有多大。低的学习率会使得学习过程运行的更慢一些（更多的训练迭代获得更符合数据的系数），而高的学习率将会加速学习过程但是将会导致最终的模型可能在正确值周围摇摆。简单的说，你既想要学的快，又想要学的好，这是不可能的。

下面的代码就创建了一个学习率为0.5的SGD优化器。

const learningRate = 0.5;
const optimizer = tf.train.sgd(learningRate);

定义训练循环

既然我们已经定义了损失函数和优化器，那么现在我们就可以创建一个训练迭代器了，它会不断地运行SGD优化器来使不断修正、完善模型的系数来减小损失（MSE）。下面就是我们创建的训练迭代器：

function train(xs, ys, numIterations = 75) {

  const learningRate = 0.5;
  const optimizer = tf.train.sgd(learningRate);

  for (let iter = 0; iter < numIterations; iter++) {
    optimizer.minimize(() => {
      const predsYs = predict(xs);
      return loss(predsYs, ys);
    });
  }

现在，让我们一步一步地仔细看看上面的代码。首先，我们定义了训练函数，并且以数据中x和y的值以及制定的迭代次数作为输入：

function train(xs, ys, numIterations) {
...
}

接下来，我们定义了之前讨论过的学习率（learning rate）以及SGD优化器：

const learningRate = 0.5;
const optimizer = tf.train.sgd(learningRate);

最后，我们定义了一个for循环，这个循环会运行numIterations次训练。在每一次迭代中，我们都调用了optimizer优化器的minimize函数，这就是见证奇迹的地方：

for (let iter = 0; iter < numIterations; iter++) {
  optimizer.minimize(() => {
    const predsYs = predict(xs);
    return loss(predsYs, ys);
  });
}

minimize 接受了一个函数作为参数，这个函数做了下面的两件事情：

1、首先它对所有的x值通过我们在之前定义的pridict函数预测了y值。

2、然后它通过我们之前定义的损失函数返回了这些预测的均方误差。

minimize函数之后会自动调整这些变量（即系数a、b、c、d）来使得损失函数更小。

在运行训练迭代器之后，a、b、c以及d就会是通过模型75次SGD迭代之后学习到的结果了。

查看结果！

一旦程序运行结束，我们就可以得到最终的a、b、c和d的结果了，然后使用它们来绘制曲线，如下所示：

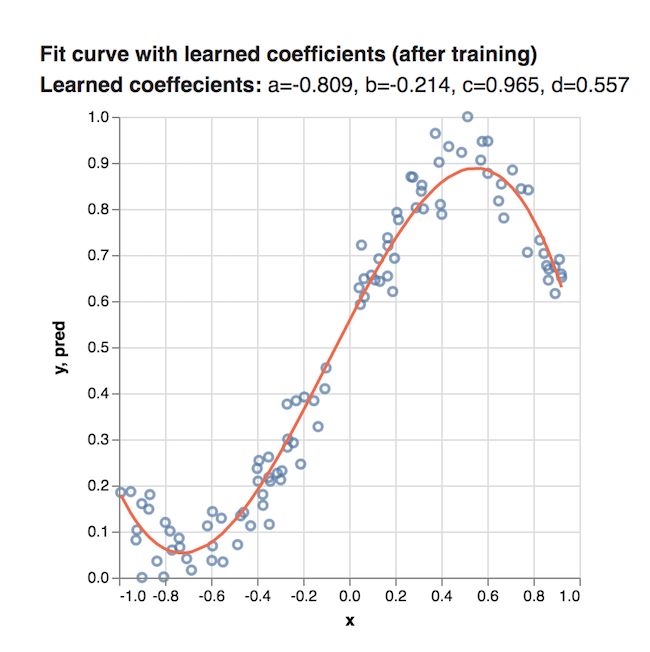
这个结果已经比开始随机分配系数的结果拟合的好得多了！

w3cschool 编程狮，随时随地学编程

Tensorflow.js 拟合曲线

先决条件

运行代码

输入数据

学习步骤

第1步：设置变量

第2步：建立模型

第3步：训练模型

定义损失函数

即这个损失函数返回的就是一个均方差，如果这个损失函数的值越小，显然数据和系数就拟合的越好。

定义优化器

定义训练循环

查看结果！

Tensorflow.js 核心概念

Tensorflow.js 实战训练