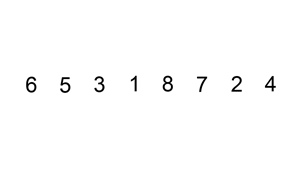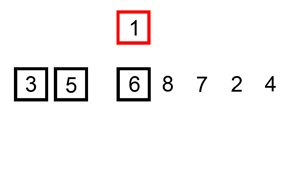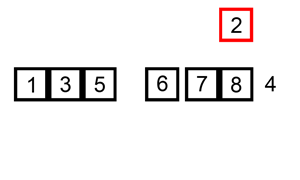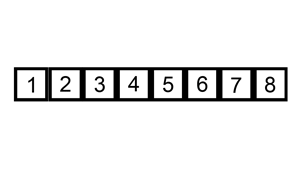(5)插入排序 (Insertion Sort)
算法原理
设有一组关键字{K1, K2,…, Kn};排序开始就认为 K1 是一个有序序列;让 K2 插入上述表长为 1 的有序序列,使之成为一个表长为 2 的有序序列;然后让 K3 插入上述表长为 2 的有序序列,使之成为一个表长为 3 的有序序列;依次类推,最后让 Kn 插入上述表长为 n-1 的有序序列,得一个表长为 n 的有序序列。
具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤 2~5
如果比较操作的代价比交换操作大的话,可以采用二分查找法来减少比较操作的数目。该算法可以认为是插入排序的一个变种,称为二分查找排序。
二分查找法,是一种在有序数组中查找某一特定元素的搜索算法。搜素过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜素过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。
实例分析
现有一组数组 arr = [5, 6, 3, 1, 8, 7, 2, 4],共有八个记录,排序过程如下:
[5] 6 3 1 8 7 2 4
↑ │
└───┘
[5, 6] 3 1 8 7 2 4
↑ │
└────────┘
[3, 5, 6] 1 8 7 2 4
↑ │
└──────────┘
[1, 3, 5, 6] 8 7 2 4
↑ │
└──┘
[1, 3, 5, 6, 8] 7 2 4
↑ │
└────┘
[1, 3, 5, 6, 7, 8] 2 4
↑ │
└────────────────┘
[1, 2, 3, 5, 6, 7, 8] 4
↑ │
└─────────────┘
[1, 2, 3, 4, 5, 6, 7, 8]其中有一点比较有意思的是,在每次比较操作发现新元素小于等于已排序的元素时,可以将已排序的元素移到下一位置,然后再将新元素插入该位置,接着再与前面的已排序的元素进行比较,这样做交换操作代价比较大。还有一个做法是,将新元素取出,从左到右依次与已排序的元素比较,如果已排序的元素大于新元素,那么将该元素移动到下一个位置,接着再与前面的已排序的元素比较,直到找到已排序的元素小于等于新元素的位置,这时再将新元素插入进去,就像下面这样:
JavaScript 语言实现
直接插入排序 JavaScript 实现代码:
function insertionSort(array) {
function swap(array, i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}
var length = array.length,
i,
j;
for (i = 1; i < length; i++) {
for (j = i; j > 0; j--) {
if (array[j - 1] > array[j]) {
swap(array, j - 1, j);
} else {
break;
}
}
}
return array;
}下面这种方式可以减少交换次数:
function insertionSort(array) {
var length = array.length,
i,
j,
temp;
for (i = 1; i < length; i++) {
temp = array[i];
for (j = i; j >= 0; j--) {
if (array[j - 1] > temp) {
array[j] = array[j - 1];
} else {
array[j] = temp;
break;
}
}
}
return array;
}利用二分查找法实现的插入排序,二分查找排序:
function insertionSort2(array) {
function binarySearch(array, start, end, temp) {
var middle;
while (start <= end) {
middle = Math.floor((start + end) / 2);
if (array[middle] < temp) {
if (temp <= array[middle + 1]) {
return middle + 1;
} else {
start = middle + 1;
}
} else {
if (end === 0) {
return 0;
} else {
end = middle;
}
}
}
}
function binarySort(array) {
var length = array.length,
i,
j,
k,
temp;
for (i = 1; i < length; i++) {
temp = array[i];
if (array[i - 1] <= temp) {
k = i;
} else {
k = binarySearch(array, 0, i - 1, temp);
for (j = i; j > k; j--) {
array[j] = array[j - 1];
}
}
array[k] = temp;
}
return array;
}
return binarySort(array);
}