
(2)快速排序 (Quick Sort)
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
算法描述快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。
动图演示
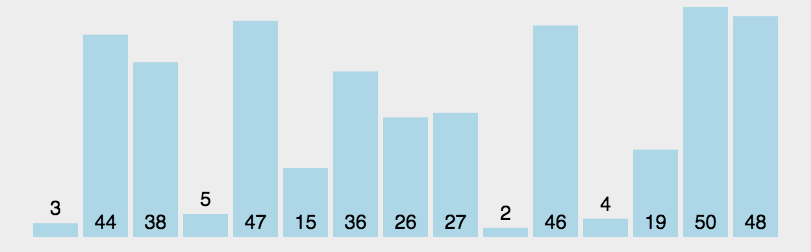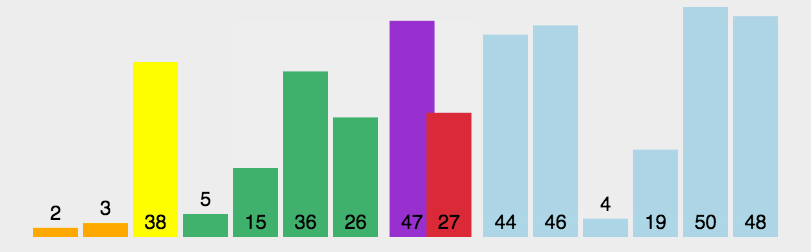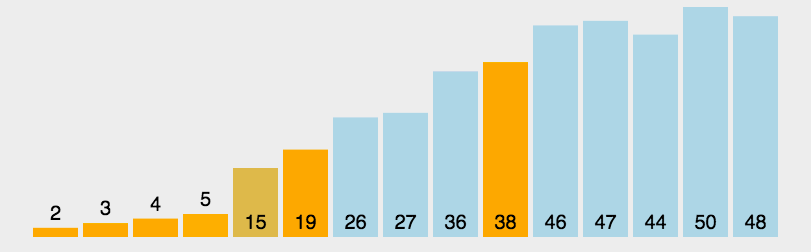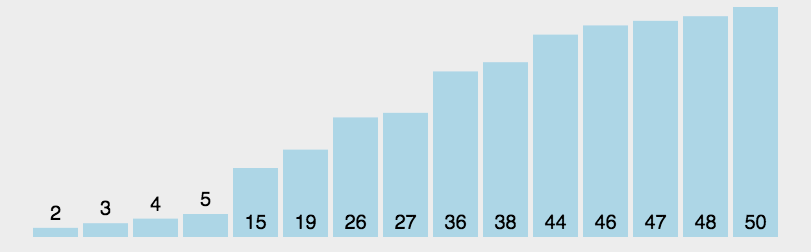
代码实现
class Solution:
def partition(self, nums, begin, end):
pivot, counter = end, begin
# counter 记录小于pivot的位置和个数
for i in range(begin, end):
if nums[i] < nums[pivot]:
counter += 1
if counter != i:
temp = nums[counter]
nums[counter] = nums[i]
nums[i] = temp
temp = nums[pivot]
nums[pivot] = nums[counter]
nums[counter] = temp
return counter
def quicksort(self, nums, begin, end):
if end <= begin: return
pivot = self.partition(nums, begin, end)
self.quicksort(nums, begin, pivot - 1)
self.quicksort(nums, pivot + 1, end)
def sortArray(self, nums: List[int]) -> List[int]:
self.quicksort(nums, 0, len(nums) - 1)
return nums算法特性- 时间复杂度(最好):O ( n l o g n ) O(nlog n)O(nlogn)
- 时间复杂度(最坏):O ( n 2 ) O(n^2)O(n2)
- 时间复杂度(平均):O ( n l o g n ) O(nlog n)O(nlogn)
- 空间复杂度:O ( n l o g n ) O(nlog n)O(nlogn)
- 稳定性:不稳定
算法原理
- 时间复杂度(最好):O ( n l o g n ) O(nlog n)O(nlogn)
- 时间复杂度(最坏):O ( n 2 ) O(n^2)O(n2)
- 时间复杂度(平均):O ( n l o g n ) O(nlog n)O(nlogn)
- 空间复杂度:O ( n l o g n ) O(nlog n)O(nlogn)
- 稳定性:不稳定
快速排序是图灵奖得主 C. R. A. Hoare 于 1960 年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。