WebGL 3D 透视

在上一篇文章中，我们就学习过如何做三维，但三维没有任何透视。它是利用一个所谓的“正交”的观点，它固然有其用途，但这通常不是人们说 “3D” 时他们想要的。

相反，我们需要补充透视。只不过什么是透视？它基本上是一种事物越远显得更小的特征。

看上面的例子，我们看到越远的东西被画得越小。鉴于我们目前样品的一个让较远的物体显得更小简单的方法就是将 clipspace X 和 Y 除以 Z。

可以这样想：如果你有一条从（10，15）到 (20,15) 的线段，10个单位长。在我们目前的样本中，它将绘制 10 像素长。但是如果我们除以 Z，例如例子中如果是 Z 是 1

10 / 1 = 10
20 / 1 = 20
abs(10-20) = 10

这将是 10 像素，如果 Z 是 2，则有

10 / 2 = 5
20 / 2 = 10
abs(5 - 10) = 5

5 像素长。如果 Z = 3，则有

10 / 3 = 3.333
20 / 3 = 6.666
abs(3.333 - 6.666) = 3.333

你可以看到，随着 Z 的增加，随着它变得越来越远，我们最终会把它画得更小。如果我们在 clipspace 中除，我们可能得到更好的结果，因为 Z 将是一个较小的数字（-1 到 +1）。如果在除之前我们加一个 fudgeFactor 乘以 Z，对于一个给定的距离我们可以调整事物多小。

让我们尝试一下。首先让我们在乘以我们的 “fudgefactor” 后改变顶点着色器除以 Z 。

<script id="2d-vertex-shader" type="x-shader/x-vertex">
...
uniform float u_fudgeFactor;
...
void main() {
  // Multiply the position by the matrix.
  vec4 position = u_matrix * a_position;

  // Adjust the z to divide by
  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

  // Divide x and y by z.
  gl_Position = vec4(position.xy / zToDivideBy, position.zw);
}
</script>

注意，因为在 clipspace 中 Z 从 -1 到 +1，我加 1 得到 zToDivideBy 从 0 到 +2 * fudgeFactor

我们也需要更新代码，让我们设置 fudgeFactor。

  ...
  var fudgeLocation = gl.getUniformLocation(program, "u_fudgeFactor");

  ...
  var fudgeFactor = 1;
  ...
  function drawScene() {
    ...
    // Set the fudgeFactor
    gl.uniform1f(fudgeLocation, fudgeFactor);

    // Draw the geometry.
    gl.drawArrays(gl.TRIANGLES, 0, 16 * 6);

下面是结果。

如果没有明确的把 “fudgefactor” 从 1 变化到 0 来看事物看起来像什么样子在我们除以 Z 之前。

WebGL 在我们的顶点着色器中把 X，Y，Z，W 值分配给 gl_Position 并且自动除以 W。

我们可以证明通过改变着色这很容易实现，而不是自己做除法，在 gl_Position.w 中加 zToDivideBy 。

<script id="3d-vertex-shader" type="x-shader/x-vertex">
...
uniform float u_fudgeFactor;
...
void main() {
  // Multiply the position by the matrix.
  vec4 position = u_matrix * a_position;

  // Adjust the z to divide by
  float zToDivideBy = 1.0 + position.z * u_fudgeFactor;

  // Divide x, y and z by zToDivideBy
  gl_Position = vec4(position.xyz,  zToDivideBy);
}
</script>

看看这是完全相同的。

为什么有这样一个事实： WebGL 自动除以 W ？因为现在，使用更多维的矩阵，我们可以使用另一个矩阵复制 z 到 w。

矩阵如下

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 0,

将复制 z 到 w.你可以看看这些列如下

x_out = x_in * 1 +
        y_in * 0 +
        z_in * 0 +
        w_in * 0 ;

y_out = x_in * 0 +
        y_in * 1 +
        z_in * 0 +
        w_in * 0 ;

z_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 0 ;

w_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 0 ;

简化后如下

x_out = x_in;
y_out = y_in;
z_out = z_in;
w_out = z_in;

我们可以加 1 我们之前用的这个矩阵，因为我们知道 w_in 总是 1.0。

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 1,
0, 0, 0, 1,

这将改变 W 计算如下

w_out = x_in * 0 +
        y_in * 0 +
        z_in * 1 +
        w_in * 1 ;

因为我们知道 w_in = 1.0 所以就有

w_out = z_in + 1;

最后我们可以将 fudgeFactor 加到矩阵，矩阵如下

1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, fudgeFactor,
0, 0, 0, 1,

这意味着

w_out = x_in * 0 +
        y_in * 0 +
        z_in * fudgeFactor +
        w_in * 1 ;

简化后如下

w_out = z_in * fudgeFactor + 1;

所以，让我们再次修改程序只使用矩阵。　　　　

首先让我们放回顶点着色器。这很简单

<script id="2d-vertex-shader" type="x-shader/x-vertex">
uniform mat4 u_matrix;

void main() {
  // Multiply the position by the matrix.
  gl_Position = u_matrix * a_position;
  ...
}
</script>

接下来让我们做一个函数使 Z - > W 矩阵。

function makeZToWMatrix(fudgeFactor) {
  return [
    1, 0, 0, 0,
    0, 1, 0, 0,
    0, 0, 1, fudgeFactor,
    0, 0, 0, 1,
  ];
}

我们将更改代码，以使用它。

    ...
    // Compute the matrices
    var zToWMatrix =
        makeZToWMatrix(fudgeFactor);

    ...

    // Multiply the matrices.
    var matrix = matrixMultiply(scaleMatrix, rotationZMatrix);
    matrix = matrixMultiply(matrix, rotationYMatrix);
    matrix = matrixMultiply(matrix, rotationXMatrix);
    matrix = matrixMultiply(matrix, translationMatrix);
    matrix = matrixMultiply(matrix, projectionMatrix);
    matrix = matrixMultiply(matrix, zToWMatrix);

    ...

注意，这一次也是完全相同的。

以上基本上是向你们展示，除以 Z 给了我们透视图，WebGL 方便地为我们除以 Z。　　　　

但是仍然有一些问题。例如如果你设置 Z 到 -100 左右，你会看到类似下面的动画。

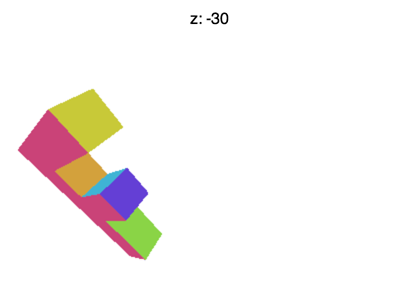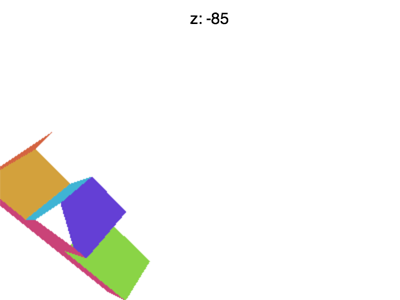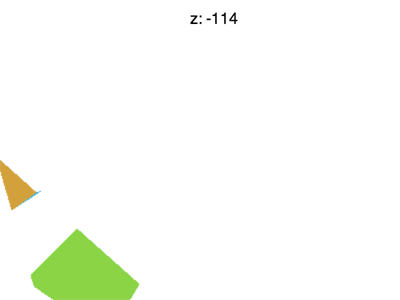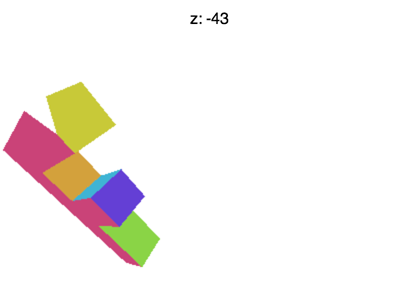
发生了什么事？为什么 F 消失得很早？就像 WebGL 剪辑 X 和 Y 或+ 1 到 - 1 它也剪辑 Z。这里看到的就是 Z＜-1 的地方。

我可以详细了解如何解决它，但你可以以我们做二维投影相同的方式来得到它。我们需要利用 Z，添加一些数量和测量一定量，我们可以做任何我们想要得到的 -1 到 1 的映射范围。

真正酷的事情是所有这些步骤可以在 1 个矩阵内完成。甚至更好的，我们来决定一个 fieldOfView 而不是一个 fudgeFactor，并且计算正确的值来做这件事。

这里有一个函数来生成矩阵。

function makePerspective(fieldOfViewInRadians, aspect, near, far) {
  var f = Math.tan(Math.PI * 0.5 - 0.5 * fieldOfViewInRadians);
  var rangeInv = 1.0 / (near - far);

  return [
    f / aspect, 0, 0, 0,
    0, f, 0, 0,
    0, 0, (near + far) * rangeInv, -1,
    0, 0, near * far * rangeInv * 2, 0
  ];
};

这个矩阵将为我们做所有的转换。它将调整单位，所以他们在clipspace 中它会做数学运算，因此我们可以通过角度选择视野，它会让我们选择我们的 z-clipping 空间。它假定有一个 eye 或 camera 在原点（0，0，0）并且给定一个 zNear 和 fieldOfView 计算它需要什么，因此在 zNear 的物体在 z = - 1 结束以及在 zNear 的物体它们在中心以上或以下半个 fieldOfView，分别在 y = - 1 和 y = 1 结束。计算 X 所使用的只是乘以传入的 aspect。我们通常将此设置为显示区域的 width / height。最后，它计算出在 Z 区域物体的规模，因此在 zFar 的物体在 z = 1 处结束。

下面是动作矩阵的图。

形状像四面锥的立方体旋转称为“截锥”。矩阵在截锥内占空间并且转换到 clipspace。zNear 定义夹在前面的物体，zfar定义夹在后面的物体。设置 zNear 为23你会看到旋转的立方体的前面得到裁剪。设置 zFar 为24你会看到立方体的后面得到剪辑。

只剩下一个问题。这个矩阵假定有一个视角在 0，0，0 并假定它在Z轴负方向，Y的正方向。我们的矩阵到目前为止已经以不同的方式解决问题。为了使它工作，我们需要我们的对象在前面的视图。

我们可以通过移动我们的 F 做到。 我们在（45，150，0）绘图。让我们将它移到（0，150，- 360）

现在，要想使用它，我们只需要用对 makePerspective 的调用取代对make2DProjection 旧的调用

    var aspect = canvas.clientWidth / canvas.clientHeight;
    var projectionMatrix =
        makePerspective(fieldOfViewRadians, aspect, 1, 2000);
    var translationMatrix =
        makeTranslation(translation[0], translation[1], translation[2]);
    var rotationXMatrix = makeXRotation(rotation[0]);
    var rotationYMatrix = makeYRotation(rotation[1]);
    var rotationZMatrix = makeZRotation(rotation[2]);
    var scaleMatrix = makeScale(scale[0], scale[1], scale[2]);

结果如下

我们回到了一个矩阵乘法，我们得到两个领域的视图，我们可以选择我们的 z 空间。受篇幅限制我们没有做。下一节，摄像机。