
三灯游戏
三灯游戏的规则
请在下述情况时按下按钮:
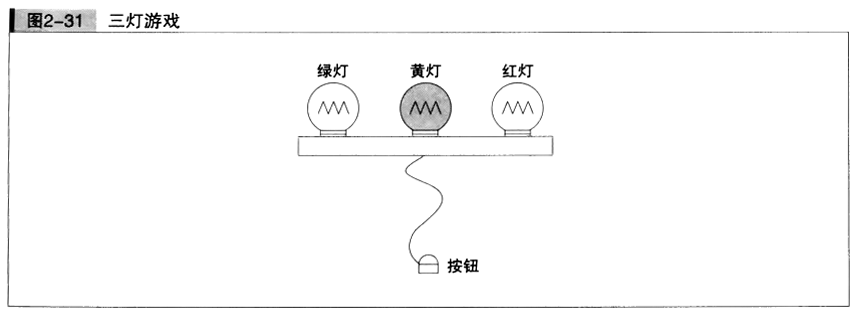
现在灯泡有绿色、黄色、红色三种(图2-31)。
这回光靠脑袋想可不行了。还是使用卡诺图看看吧(图2-32)。假设有以下命题:
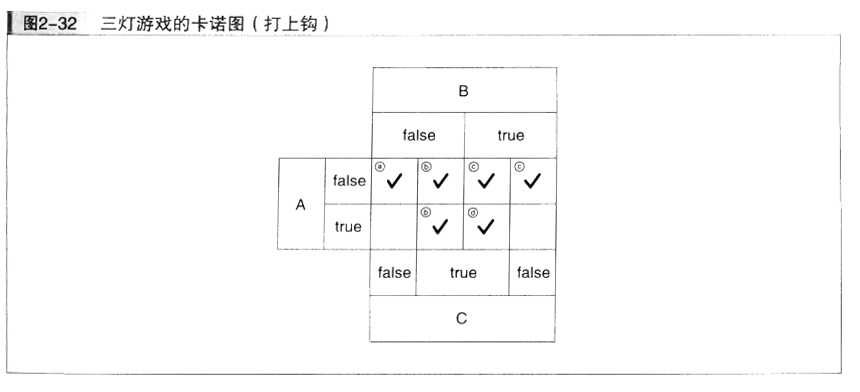
画出A、B、C的true/false所有组合的表,在“应该按下按钮”之处打上勾。这次有三个命题,因此表的网格数变为2³=8个。
注意一下B和C的false/true分界是错位的。正是这个“错位”,使得用8个网格就能表示所有情况。
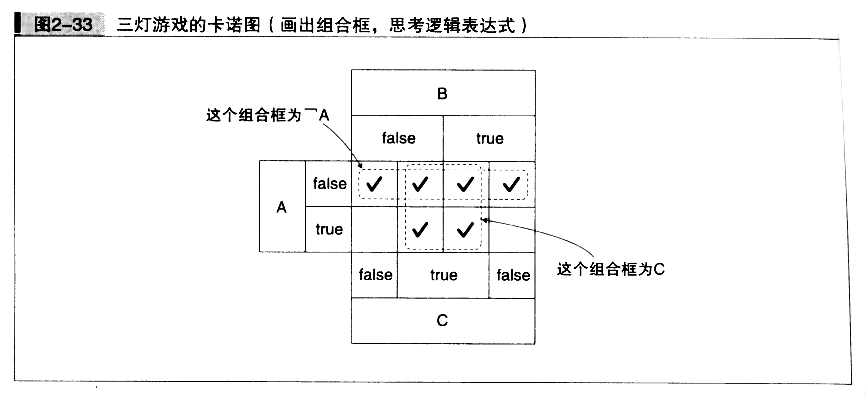
打上勾后,就像前面那样尽可能用大的框进行分组(图2-33)。
将所有打钩处都框起来后,我们来看看表示各个组合框的逻辑表达式吧。
横向的组合框,就是A为ifalse的区域,因此用¬A和C的逻辑或来表示,即
三灯游戏的规则看起来相当复杂,然而通过使用卡诺图,居然能够大幅简化它的表现形式。不可思议吧!
最后得到的逻辑表达式为(¬A)∨C,表明在三灯游戏中,当“绿灯灭(¬A)”或者“红灯亮(C)”的时候可以按下按钮。
在这个逻辑表达式中没有出现B。由此我们可知,在判断是否按下按钮时,不需要看黄灯。卡诺图通常用于简化逻辑表达式、设计逻辑电路等。
请在下述情况时按下按钮:
- 绿灯、黄灯、红灯都灭
- 黄灯灭,红灯亮
- 绿灯灭,黄灯亮
- 绿灯、黄灯、红灯都亮
现在灯泡有绿色、黄色、红色三种(图2-31)。
这回光靠脑袋想可不行了。还是使用卡诺图看看吧(图2-32)。假设有以下命题:
- 命题A 绿灯亮
- 命题B 黄灯亮
- 命题C 红灯亮


画出A、B、C的true/false所有组合的表,在“应该按下按钮”之处打上勾。这次有三个命题,因此表的网格数变为2³=8个。
注意一下B和C的false/true分界是错位的。正是这个“错位”,使得用8个网格就能表示所有情况。
打上勾后,就像前面那样尽可能用大的框进行分组(图2-33)。
将所有打钩处都框起来后,我们来看看表示各个组合框的逻辑表达式吧。
横向的组合框,就是A为ifalse的区域,因此用¬A和C的逻辑或来表示,即
(¬A)∨C
三灯游戏的规则看起来相当复杂,然而通过使用卡诺图,居然能够大幅简化它的表现形式。不可思议吧!

最后得到的逻辑表达式为(¬A)∨C,表明在三灯游戏中,当“绿灯灭(¬A)”或者“红灯亮(C)”的时候可以按下按钮。
在这个逻辑表达式中没有出现B。由此我们可知,在判断是否按下按钮时,不需要看黄灯。卡诺图通常用于简化逻辑表达式、设计逻辑电路等。