题目

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。即使有多个不同答案，你也只需要返回其中一种。

格雷编码序列必须以 0 开头。

示例 1:

输入: 2
输出: [0,1,3,2]
解释:


00 - 0
01 - 1
11 - 3
10 - 2

对于给定的 n，其格雷编码序列并不唯一。 例如，[0,2,3,1] 也是一个有效的格雷编码序列。

00	0
10	2
11	3
01	1

示例 2:

输入: 0
输出: [0]

解释: 我们定义格雷编码序列必须以 0 开头。 给定编码总位数为 n 的格雷编码序列，其长度为 2n。当 n = 0 时，长度为 20 = 1。 因此，当 n = 0 时，其格雷编码序列为 [0]。

解题

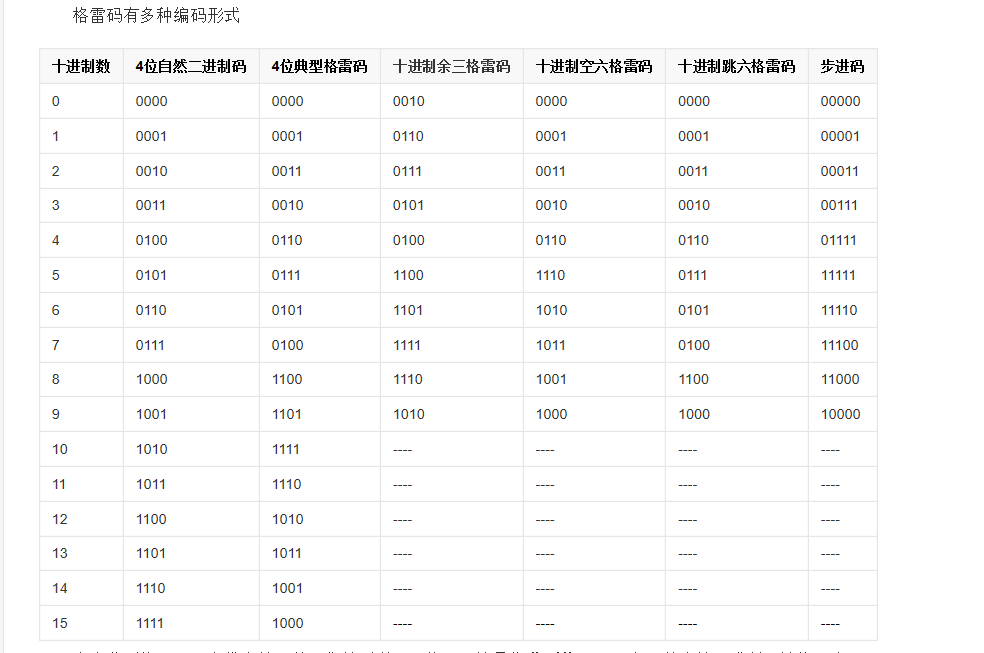
1.二进制码→格雷码（编码）：

此方法从对应的n位二进制码字中直接得到n位格雷码码字，步骤如下： 对n位二进制的码字，从右到左，以0到n-1编号 如果二进制码字的第i位和i+1位相同，则对应的格雷码的第i位为0，否则为1（当i+1=n时，二进制码字的第n位被认为是0，即第n-1位不变）

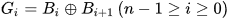
2.格雷码→二进制码（解码）：

从左边第二位起，将每位与左边一位解码后的值异或，作为该位解码后的值（最左边一位依然不变）。依次异或，直到最低位。依次异或转换后的值（二进制数）就是格雷码转换后二进制码的值。

class Solution {
    public List<Integer> grayCode(int n) {
        List<Integer> res = new ArrayList<Integer>() {{ add(0); }};
        int head = 1;
        for (int i = 0; i < n; i++) {
            for (int j = res.size() - 1; j >= 0; j--)
                res.add(head + res.get(j));
            head <<= 1;
        }
        return res;
    }
}

方法解析

1.head <<= 1; x<<=1等于x=x<<1，是把x左移1位以后值保存回x里，x发生变化了。