费马小定理(Fermat's little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）。

引理1

若a，b，c为任意3个整数,m为正整数，且(m,c)=1，则当a·c≡b·c(mod m)时，有a≡b(mod m)。 证明：a·c≡b·c(mod m)可得ac–bc≡0(mod m)可得(a-b)·c≡0(mod m)。因为(m,c)=1即m,c互质，c可以约去，a– b≡0(mod m)可得a≡b(mod m)。

引理2

设m是一个整数且m>1，b是一个整数且(m,b)=1。如果a[1],a[2],a[3],a[4],…a[m]是模m的一个完全剩余系，则b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]也构成模m的一个完全剩余系。 　　证明：若存在2个整数b·a[i]和b·a[j]同余即b·a[i]≡b·a[j](mod m)..(i>=1 && j>=1)，根据引理1则有a[i]≡a[j](mod m)。根据完全剩余系的定义可知这是不可能的，因此不存在2个整数b·a[i]和b·a[j]同余。 所以b·a[1],b·a[2],b·a[3],b·a[4],…b·a[m]构成模m的一个完全剩余系。 构造素数 的完全剩余系 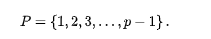因为 ，由引理2可得 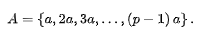也是p的一个完全剩余系。由完全剩余系的性质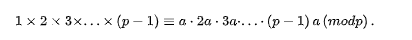， 即 易知 ，同余式两边可约去 ，得到 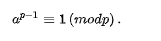这样就证明了费马小定理

例子

应用

应用 费马小定理可以快速求得x关于p的逆元

前提当然得是x与p互质才有逆元。

即：x*x^p-2 ≡ 1 （mod p）

所以x^p-2就是x关于p的逆元。

C++代码实现

求逆元的代码实现 这里使用了快速幂算法来求x^p-2。

#include<iostream>
#define ll long long
using namespace std;
ll quickpow(ll a, ll b, ll p){
    ll temp = 1;
    while(b){
        if(b & 1) temp = (temp * a) % p;
        a = (a * a) % p;
        b >>= 1;
    }
    return temp;
}
int main()
{
    ll a, p;
    cin>>a>>p;
    cout<<quickpow(a, p-2, p)<<endl;
    return 0;
}