
密码学 希尔密码
简介
希尔密码(Hill Cipher)是运用基本矩阵论原理的替换密码,由Lester S. Hill在1929年发明。每个字母当作26进制数字:A=0, B=1, C=2... 一串字母当成n维向量,跟一个n×n的矩阵相乘,再将得出的结果MOD26。
解析
对于密码体制的五元组(P, C, K, E, D)有 P=C=(Z26)m,m是一个不小于2的正整数
- K是定义在Z26上的m×m可逆矩阵的集合
- 取密钥k∈K,k为一个m×m矩阵,记为(kij),对
x=(x1,x2,...,xm)∈P, y= (y1,y2,...,ym)∈C,定义
- ek(x)=xk
- dk(y)=yk-1 k-1表示k的逆矩阵
- 以上运算均在Z26上运行(模26)

例题
题目
在线代的课本上出现了一堆神秘字母
dloguszijluswogany
而旁边的矩阵是
1 2 0 1
快找出flag吧
key格式:simCTF{}
解答
1.求矩阵M= 1 2 0 1 的逆矩阵 即 M^-1= 1 -2 0 1
求逆矩阵方法:
1、伴随矩阵:伴随矩阵是矩阵元素所对应的代数余子式,所构成的矩阵,转置后得到的新矩阵。
2、初等变换:写出增广矩阵A|E,即矩阵M右侧放置一个同阶的单位矩阵,得到一个新矩阵。然后进行初等行变换,将增广矩阵的左侧变换为一个同阶单位矩阵,这时右侧为所求M的逆矩阵。
2、根据字母表顺序将密文换成矩阵数值
| d | l | o | g | u | s | z | i | j | l | u | s | w | o | g | a | n | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 12 | 15 | 7 | 21 | 19 | 26 | 9 | 10 | 12 | 21 | 19 | 23 | 15 | 7 | 1 | 14 | 25 |
3、将密钥的逆矩阵与密文变换成的矩阵做乘运算

4、将得到的矩阵mod26
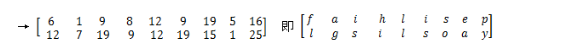
5.可求明文:flagis hillissoeasy所以simCTF{hillissoeapy}
实现
使用numpy库的矩阵对象,可以十分方便地进行矩阵乘法,矩阵求逆和取模等运算。
import numpy as np
m = 'YOURPINNOISFOURONETWOSIX' #明文
a = np.matrix([[11,2,19],[5,23,25],[20,7,17]]) #密钥LCTFXZUHR
num_m = []
temp = []
count = 1
for i in m: #将明文分为三个一组
temp.append(ord(i)-ord('A'))
if count % 3 == 0:
num_m.append(temp)
temp = []
count += 1
mat_m = [np.matrix(i).T for i in num_m] #将明文分组转换为向量形式
mat_c = [a * i % 26 for i in mat_m] #得到密文分组的向量形式
num_c = []
temp = []
for i in mat_c: #将密文向量转换为列表形式,且合并到一个列表
temp = i.tolist()
for j in range(3):
num_c.append(temp[j][0])
c = [chr(i+ord('A')) for i in num_c]
print(''.join(c)) #连接成字符串,输出密文