简介

恺撒移位密码 因据说恺撒是率先使用加密函的古代将领之一，因此这种加密方法被称为恺撒密码。这是一种简单的加密方法，这种密码的密度是很低的，只需简单地统计字频就可以破译。 现今又叫“移位密码”，只不过移动的位数不一定是3位而已。

故事

将替换密码用于军事用途的第一个文件记载是恺撒著的《高卢记》。恺撒描述了他如何将密信送到正处在被围困、濒临投降的西塞罗。其中罗马字母被替换成希腊字母使得敌人根本无法看懂信息。 苏托尼厄斯在公元二世纪写的《恺撒传》中对恺撒用过的其中一种替换密码作了详细的描写。恺撒只是简单地把信息中的每一个字母用字母表中的该字母后的第三个字母代替。这种密码替换通常叫做恺撒移位密码，或简单的说，恺撒密码。 尽管苏托尼厄斯仅提到三个位置的恺撒移位，但显然从1到25个位置的移位我们都可以使用， 因此，为了使密码有更高的安全性，单字母替换密码就出现了。 如： 明码表 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 密码表 Q W E R T Y U I O P A S D F G H J K L Z X C V B N M 明文 F O R E S T 密文 Y G K T L Z 只需重排密码表二十六个字母的顺序，允许密码表是明码表的任意一种重排，密钥就会增加到四千亿亿亿多种，我们就有超过4×1027种密码表。破解就变得很困难。

详解

加密时每一个字母向前推移 k 位，例如当 k=5 时，置换表如下图：

于是我们把每个字母对应一个数字分别从0~25

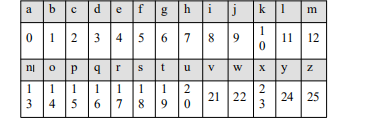
则 Caesar 加密变换实际上是： c = (m + k) mod 26 其中 m 是明文对应的数据，c 是与明文对应的密文数据，k 是加密用的参数，也称为密钥。 很容易得到相应的 Caesar 解密变换是： m = D(c) = (c – k) mod 26

例子

1.手动完成 Caesar 密码 当密钥 k=3 时，对应明文：data security has evolved rapidly 的密文：GDWD VHFXULWB KDV HYROYHG UDSL 2.Caesar 加密 编码实现“Caesar 密码”。在明文输入区输入明文：data security has evolved rapidly。将密钥 k 调节到 3，查看相应的密文，并与你手动加密的密文进行比较。 m = D(c) = (c – k) mod 26

C++代码

#include < iostream >
using namespace std;
int main() {
    char c[27] = {       'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z',' '
    };
    char mi[27];
    int a = 1,
    b = 3;
    int i = 0;
    for (i = 0; i < 26; i++) {
        mi[i] = c[(b + i * a) % 26]; //按顺序对应的密码
    }
    char in [1024] = {
        '/0'
    };
    mi[26] = {
        ' '
    };
    gets_s( in );
    for (i = 0; i < 10; i++) cout << in[i];
    for (i = 0; i < 26; i++) {
        cout << c[i] << mi[i] << endl;
    }
    cout << "解密为:" << endl;
    int k;
    for (k = 0; k < 30; k++) {
        for (i = 0; i <= 26; i++) {
            if ( in [k] == mi[i]) {
                cout << c[i];
                break;
            }
        }
    }
    cout << "加密为" << endl;
    for (k = 0; k < 30; k++) {
        for (i = 0; i <= 26; i++) {
            if ( in [k] == c[i]) {
                cout << mi[i];
                break;
            }
        }
    }
}