Assembly 浮点表示法
非整形的二进制数
在第一章讨论数制的时候，我们只讨论了整形。显然，和十进制一样，其它进制必须也能表示非整形数。在十进制中，在小数点右边的数字关联了10的负乘方值：
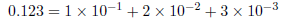
不必惊讶，二进制也是以同样的方法表示：
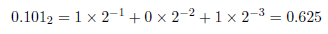
这个办法与第一章中的整形办法相结合就可以用来转换一个一般数值：
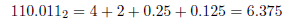
将十进制转换成二进制也不是很难。一般来说，需将十进制数分成两块：整数部分和分数部分。使用第一章中的方法来将整数部分转换成二进制。分数部分的转换可以使用下面描述的方法。
考虑一个用a、b、c···标记比特位的二进制分数。这个数用二进制表示为：
0.abcdef...
将此数乘2.新得到的数的二进制表示将是：
a.bcdef...
注意，第一个比特位现在在权值为1的位置。用0替换a得到：
0.bcdef...
再乘以2得到：
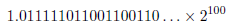
Intel数学协处理器使用第三种，更高的精度，称为扩展精度。事实上，在数学协处理器自身里的所有数据都是这种格式。当数据从协处理器储存到内存中时，将自动转换成单或双精度。跟IEEE的浮点双精度格式相比，扩展精度使用了一种有细微差别的格式，所以将不在这讨论。
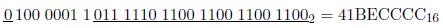
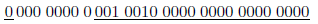
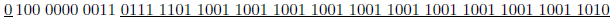
b.cdef...
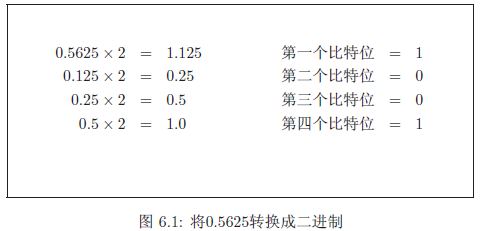
现在第二个比特位(b)在权值为1的位置。重复这个过程，直到得到了需要的尽可能多的比特位。图6.1展示了一个实例：将0.5625转换成二进制。这种方法当分数部分为0了才停止。
另一个例子，将23.85转换成二进制。将整数部分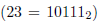
转换成二进制是容易的，但是分数部分呢？图6.2展示了这个计算的开始部分。如果你仔细看了这个数值，就会发现一个无限循环。这就意味着0.85是一个无限循环的二进制数(与基数为10的无限循环十进制数相对应)。这里显示了这个数的计算模式。在这个模式中，你可以看到
。因此，
。
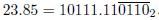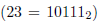转换成二进制是容易的，但是分数部分呢？图6.2展示了这个计算的开始部分。如果你仔细看了这个数值，就会发现一个无限循环。这就意味着0.85是一个无限循环的二进制数(与基数为10的无限循环十进制数相对应)。这里显示了这个数的计算模式。在这个模式中，你可以看到。因此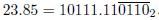，。上面计算的一个重要结论是23.85不可以用有限的比特位来精确表示成二进制数。(就像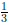
不能表示成有限的十进制数。)正如这一章展示的，C语言中的float和double变量是以二进制储存的。因此，类似23.85的数值不能精确地储存到这些变量中。只能储存23.85的近似值。
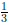不能表示成有限的十进制数。)正如这一章展示的，C语言中的float和double变量是以二进制储存的。因此，类似23.85的数值不能精确地储存到这些变量中。只能储存23.85的近似值。为了简化硬件，采用固定的格式来储存浮点数。这种格式采用科学计数法(但是是在二进制中，是2的乘方,不是10)。例如，23.85或10111.11011001100110...₂将储存为：
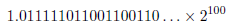
(其中指数(100)是二进制形式)。规范的浮点数有下面的形式：
其中1:sssssssssssss是有效数而eeeeeeee是指数。
IEEE浮点表示法
IEEE(Institute of Electrical and Electronic Engineers，电气与电子工程师学会)是一个国际组织，它已经设计了存储浮点数的特殊的二进制格式。这种格式应用在大多数(但不是全部)现在的电脑上。通常电脑本身的硬件就支持它。例如，Intel的数学协处理器(从Pentium开始，就嵌入到所有它的CPU中了)就使用它。IEEE为不同的精度定义了不同的格式：单或双精度。在C语言中，float变量使用单精度，而double变量使用双精度。
Intel数学协处理器使用第三种，更高的精度，称为扩展精度。事实上，在数学协处理器自身里的所有数据都是这种格式。当数据从协处理器储存到内存中时，将自动转换成单或双精度。跟IEEE的浮点双精度格式相比，扩展精度使用了一种有细微差别的格式，所以将不在这讨论。
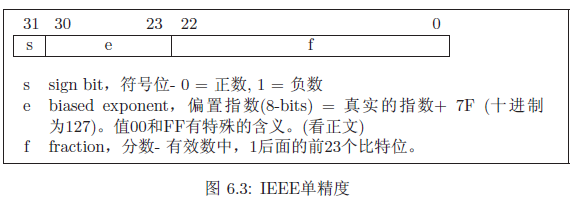
IEEE单精度
单精度浮点使用32个比特位来编码数字。通常它精确到小数点后七位。相比于整数，浮点数的储存格式更复杂。图6.3展示了IEEE单精度数的基本格式。这种格式有几个古怪的地方。负的浮点数并不使用补码表示法。它们使用符号量值表示法。如图显示，第31位决定数的符号。二进制的指数并不会直接储存。取而代之的是将指数和7F的和储存到位23 30中。这个偏置指数总是非负的。
分数部分假定是一个规范的有效数(格式为1:sssssssss)。因为第一个比特位总是1,所以领头的1是不储存的！这就允许在后面储存一额外的比特位，稍微地扩展了精度。这个想法称为隐藏一的表示法。
怎样储存23.85呢？ 首你必须永远记住：这些字 先，它是个正数，所以符号位为0。其次，真实的指数为4,所以偏置指数为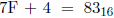
。最后，分数部分应表示为01111101100110011001100 (记住领头的1是隐藏的)。把这些放到一起得到(为了帮助澄清浮点格式的不同部分，符号位和分数部分都加了下划线，而且所有的比特位都分成了四个比特位一组。)：
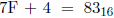。最后，分数部分应表示为01111101100110011001100 (记住领头的1是隐藏的)。把这些放到一起得到(为了帮助澄清浮点格式的不同部分，符号位和分数部分都加了下划线，而且所有的比特位都分成了四个比特位一组。)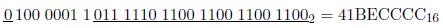：这不是准确的23.85(因为它是一个无限循环的二进制数)。如果你将上面的数值转换回十进制形式，你会发现它大约等于23.849998474。这个数与23.85非常接近，但是它并不准确。实际上，在C语言中，23.85的描述和上面的是一样的。因为该数的精确描述被截去后的最左边的位为1,所以最后一个比特位经四舍五入后为1。因此单精度数23.85将表示成十六进制41 BE CC CD。将这个转换成十进制得23.850000381，这个数就更接近23.85。怎么描述-23.85呢？只需要改变符号位得：C1 BE CC CD。不要使用补码！
IEEE浮点格式中，e和f 的某些组合有特殊的含义。表6.1描述了这些特殊的值。溢出或除以0将产生一个无穷数。一个无效的操作将产生一个不确定的结果，例如：试图求一个负数的平方根，将两个无穷数相加，等等。规范的单精度数的数量级范围为从
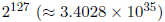
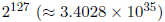
非规范化数
非规范化数可以用来表示那些值太小了以致于不能以规范格式描述的数(也就是小于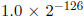
)。例如：考虑下数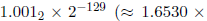
。在约定的规范格式中，这个指数太小了。但是，它可以用非规范的格式来描述：
。为了储存这个数，偏置指数被置为0(看表6.1)，而且分数部分是以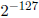
方式书写得到的所有有效数(也就是说储存了所有的比特位，包括小数点左边的1).
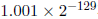将表示成：
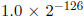)。例如：考虑下数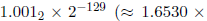。在约定的规范格式中，这个指数太小了。但是，它可以用非规范的格式来描述：。为了储存这个数，偏置指数被置为0(看表6.1)，而且分数部分是以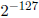方式书写得到的所有有效数(也就是说储存了所有的比特位，包括小数点左边的1).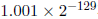将表示成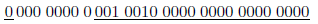：IEEE双精度
IEEE双精度使用64位来表示数字，而且通常精确到小数点后15位。如图6.4所示，基本的结构和单精度是非常相似的。只是相比于单精度，它使用了更多的位来描述偏置指数(11)和分数(52)。
更大范围的偏置指数会导致两个后果。一是计算的将是真实指数和3FF(1023)的和(而不是单精度中的7F)。二是，允许描述更大范围的真实的指数(因此也可以描述更大范围的数量级)。双精度的数量级范围大约为从
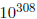到
。
到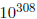。双精度值中增加的有效位是增大分数字段的原因。
作为一个例子，再次考虑下。偏置指令用十六进制表示为4 + 3FF =403。因此，该数用双精度表示为：
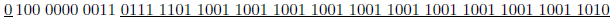
或在十六进制中为40 37 D9 99 99 99 99 9A。如果你将它转换回十进制，你将得到23.8500000000000014 (这有12个0！)，这个数就更接近23.85。
双精度和单精度一样有一些特殊的值3。非规范化数同样也是一样的。
最主要的区别是双精度的非规范数使用
。
最主要的区别是双精度的非规范数使用
。