
Assembly 浮点运算
电子计算机里的浮点运算和持续精确的数学运算是不同的。数学中,所有的数都可以精确表示。但就如前面的章节所示,在电子计算机里,许多数不能用有限个比特位来描述。所有的计算都在一定的精度下执行。在这节的例子中,为了简单化,将使用8位的有效数。
加法
要将两个浮点数相加,它们的指数必须是相等的。如果它们并不相等,那么通过移动较小指数的数的有效数来使它们相等。例如:考虑10.375 +6.34375 = 16.71875或在十进制中:

这两个数字的指数不一样,所以通过移动有效数使指数相同,然后再相加:

注意,移位丢掉了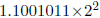 中的末尾的1,经过四舍五入后得
中的末尾的1,经过四舍五入后得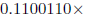
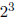 。加法的结果,
。加法的结果,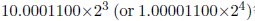 等于10000.110₂或16.75。这个数并不等于准确的答案(16.71875)!它只是一个近似值,是在进行加法操作时四舍五入后的应有误差。
等于10000.110₂或16.75。这个数并不等于准确的答案(16.71875)!它只是一个近似值,是在进行加法操作时四舍五入后的应有误差。
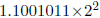 中的末尾的1,经过四舍五入后得
中的末尾的1,经过四舍五入后得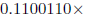
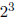 。加法的结果,
。加法的结果,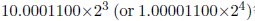 等于10000.110₂或16.75。这个数并不等于准确的答案(16.71875)!它只是一个近似值,是在进行加法操作时四舍五入后的应有误差。
等于10000.110₂或16.75。这个数并不等于准确的答案(16.71875)!它只是一个近似值,是在进行加法操作时四舍五入后的应有误差。认识到在电子计算机(或计算器)里的浮点运算得到的结果经常是近似值是非常重要的。对于电子计算机里的浮点运算,算术法则不总是对的。算术中假定的无穷精度是任何电子计算机都无法做的。例如,算术法则告诉我们(a + b) - b = a;但是,在电子计算机里,并不能完全保证它正确。
减法
减法和加法一样运作,而且有和加法一样的问题。作为一个例子,考虑16.75 - 15.9375 = 0.8125:
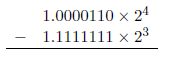
移位1.1111111 X 2³后得到(四舍五入) 1.0000000 X 


0.0000110 X 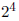 = 0.11₂ = 0.75 它并不完全正确的。
= 0.11₂ = 0.75 它并不完全正确的。
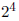 = 0.11₂ = 0.75 它并不完全正确的。
= 0.11₂ = 0.75 它并不完全正确的。乘法和除法
对于乘法,有效数执行乘法操作而指数执行相加操作。考虑10.375 X 2.5 = 25.9375:

当然,真正的结果需四舍五入成8位,得:
1.1010000 X  = 11010.0002 = 26
= 11010.0002 = 26
 = 11010.0002 = 26
= 11010.0002 = 26除法更复杂,但是也有同样的四舍五入的误差问题。
分支程序设计
这一节的重点是浮点运算的结果并不准确。程序员必须意识到这点。一个程序员经常犯的浮点运算错误就是在假定一个运算是精确的情况下,用它们去比较。例如,考虑一个执行复杂运算的f(x)函数和一个求这个函数的根的程序。你可能会试图用下面的语句来检查x是不是一个根:
if ( f (x) == 0.0 )
但是,如果f (x)返回1X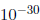 又该怎么办呢?这个数的最合适的含义是x是一个实根的非常好的近似值。可能没有一个IEEE浮点值x能恰好返回0,因为f (x)的四舍五入误差。
又该怎么办呢?这个数的最合适的含义是x是一个实根的非常好的近似值。可能没有一个IEEE浮点值x能恰好返回0,因为f (x)的四舍五入误差。
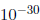 又该怎么办呢?这个数的最合适的含义是x是一个实根的非常好的近似值。可能没有一个IEEE浮点值x能恰好返回0,因为f (x)的四舍五入误差。
又该怎么办呢?这个数的最合适的含义是x是一个实根的非常好的近似值。可能没有一个IEEE浮点值x能恰好返回0,因为f (x)的四舍五入误差。一个比较好的方法是使用:
if ( fabs( f (x)) < EPS )
其中的EPS是一个宏,定义为一个非常小的正数(比如说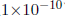 )。当f (x)非常接近0时,它就为真。一般来说,一个浮点数(譬如x)和另一个浮点数(y)的比较,需使用:
)。当f (x)非常接近0时,它就为真。一般来说,一个浮点数(譬如x)和另一个浮点数(y)的比较,需使用:
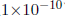 )。当f (x)非常接近0时,它就为真。一般来说,一个浮点数(譬如x)和另一个浮点数(y)的比较,需使用:
)。当f (x)非常接近0时,它就为真。一般来说,一个浮点数(譬如x)和另一个浮点数(y)的比较,需使用:if ( fabs(x ¡ y)/fabs(y) < EPS )