
MATLAB微积分
MATLAB 中有些问题需要使用微积分来解决,MATLAB提供微分方程求解任何极限的程度和计算方法,并且可以很容易地绘制图形复变函数,并检查最大值,最小值和图形解决原始函数,以及其衍生的其他内容。
在本章中,我们将讨论预演算概念,即计算功能的限制和验证的属性限制。
MATLAB计算极限
在 MATLAB 中如果要极限计算就要使用 limit 命令。其最基本的形式是将表达 limit 命令作为参数,并作为独立变量变为零发现极限的表达。
例如,让我们计算一个函数的极限 f(x) = (x3 + 5)/(x4 + 7), 当 x 趋于零。
syms x limit((x^3 + 5)/(x^4 + 7))
MATLAB执行上述语句,返回以下结果:
ans = 5/7
limit 命令属于符号计算的境界中,你需要使用 SYMS 命令告诉 MATLAB 您使用的符号变量。
limit 命令也可以计算一个函数的极限,作为变量趋于零以外的一些数字。为了计算 lim x->a(f(x)),我们使用 limit 命令参数,其中,第一个是表达式,第二个是数量,x 趋向,在这里它是a。例如,让我们计算函数极限 f(x) = (x-3)/(x-1), x 无限接近于 1.
limit((x - 3)/(x-1),1)
MATLAB执行上述语句,并返回以下结果:
ans = NaN
继续执行另外的实例,
limit(x^2 + 5, 3)
MATLAB执行上述语句,返回以下结果:
ans = 14
使用Octave计算极限
以下是上面的例子中使用 symbolic 包 Octave 版本,尝试执行和比较的结果:
pkg load symbolic
symbols
x=sym("x");
subs((x^3+5)/(x^4+7),x,0)Octave 执行上面的语句,并返回以下结果:
ans = 0.7142857142857142857
核查的基本性质限制
代数极限定理提供了一些基本的性能限制。
如下所示:
limx->p ( f(x) + g(x)) = limx->p f(x) + limx->p g(x)limx->p (f(x)- g(x)) = limx->p f(x) - limx->p g(x)limx->p (f(x)· g(x)) = limx->p f(x)· limx->p g(x)limx->p (f(x)/g(x)) = limx->p f(x)/ limx->p g(x)我们考虑两个函数:
f(x) = (3x + 5)/(x - 3)
g(x) = x2 + 1.
让我们计算为 x 的函数的极限的倾向 5,这两个函数和验证限制使用这两个函数和MATLAB的基本属性。
详细例子
在MATLAB中建立一个脚本文件,并输入下述代码:
syms x f = (3*x + 5)/(x-3); g = x^2 + 1; l1 = limit(f, 4) l2 = limit (g, 4) lAdd = limit(f + g, 4) lSub = limit(f - g, 4) lMult = limit(f*g, 4) lDiv = limit (f/g, 4)
运行该文件时,显示如下结果:
l1 = 17 l2 = 17 lAdd = 34 lSub = 0 lMult = 289 lDiv = 1
极限使用的基本性质的验证Octave
以下是上面的例子中使用 symbolic 包 Octave 版本,尝试执行和比较的结果:
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1=subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)Octave 执行上述语句,返回以下结果:
l1 = 17.0 l2 = 17.0 lAdd = 34.0 lSub = 0.0 lMult = 289.0 lDiv = 1.0
MATLAB 左,右侧极限
当一个函数具有某些特定变量的值的不连续性,极限在这一点上不存在。换句话说,极限具有不连续的函数f(x)在x = a ,当不相等的值的极限,当 x 趋向 x 从左侧的值极限为 x 的方法。
这导致的概念左手侧 和右手侧 极限。a限值定为左手侧 x > a 极限,从左侧,即 X 接近的值的 x<a。右手极限为x的极限 - 被定义为,从右边,即x接近值 x>a 。当是不相等的左手系的极限和右手极限,该极限不存在。
让我们考虑一个函数:
f(x) = (x - 3)/|x - 3|
我们将证明 limx->3 f(x) 不存在。 MATLAB帮助我们建立这个事实在两个方面:
通过绘制的函数的曲线图,并示出了不连续
通过计算的极限和显示,两者是不同的。
左手侧和右手侧极限,计算传递字符串 '左' 和 '右' limit 命令的最后一个参数。
具体示例
在MATLAB中建立一个脚本文件,并输入下述代码:
f = (x - 3)/abs(x-3); ezplot(f,[-1,5]) l = limit(f,x,3,'left') r = limit(f,x,3,'right')
运行该文件,MATLAB 得出如下的图型:
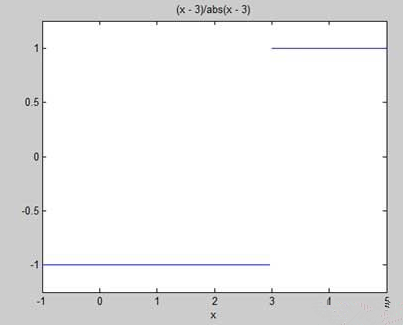
并显示下面的输出:
l = -1 r = 1