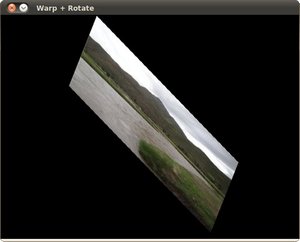
OpenCV仿射变换
目标
在本教程中,您将学习如何:
- 使用OpenCV函数cv :: warpAffine来实现简单的重映射例程。
- 使用OpenCV函数cv :: getRotationMatrix2D获得一个2×3旋转矩阵
理论
什么是仿射变换(Affine Transformations)?
- 可以以矩阵乘法(线性变换)的形式表示的转换,后跟向量加法(转换)。
- 从上面我们可以使用仿射变换表达:
- 旋转(线性变换)
- 翻译(矢量添加)
- 缩放操作(线性变换)
您可以看到,实质上,仿射变换表示两个图像之间的关系。
- 代表仿射变换的通常方法是使用2×3矩阵。
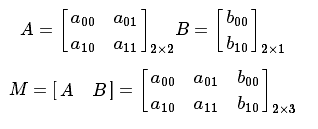
考虑到我们要使用A和B来转换2D矢量 ,我们可以这样做:
,我们可以这样做:
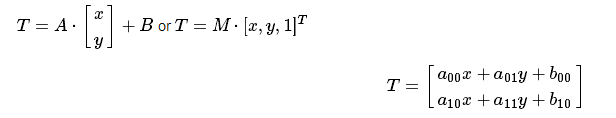
我们如何获得仿射变换?
- 我们提到仿射变换基本上是两个图像之间的关系。关于这种关系的信息大概可以通过两种方式来实现:
- 我们知道X和T,我们也知道它们是相关的。那么我们的任务就是找M
- 我们知道M和X。为了获得T,我们只需要计算T= M⋅ X。其中M的是确定的(i.e.即具有2乘3矩阵),或者它可以作为点之间的几何关系。
- 让我们以更好的方式来解释(b)。由于M和下面图像2有关,因此我们可以分析两个图像中三个点相关的最简单的情况。看下图:
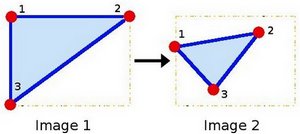
点1,2和3(在图像1中形成三角形)被映射到图像2中,仍然形成三角形,但是现在它们已经变得众所周知。如果我们发现这3个点的仿射变换(你可以根据需要选择它们),那么我们可以将这个发现的关系应用于图像中的所有像素。
Code
- 这个程序是做什么的?加载图像对图像应用仿射变换。该变换是从三点之间的关系得到的。为此,我们使用函数cv :: warpAffine。转换后对图像进行旋转。该旋转相对于图像中心等待用户退出程序
- 本教程的代码如下所示。您也可以在这里下载
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
#include <iostream>
using namespace cv;
using namespace std;
const char* source_window = "Source image";
const char* warp_window = "Warp";
const char* warp_rotate_window = "Warp + Rotate";
int main( int, char** argv )
{
Point2f srcTri[3];
Point2f dstTri[3];
Mat rot_mat( 2, 3, CV_32FC1 );
Mat warp_mat( 2, 3, CV_32FC1 );
Mat src, warp_dst, warp_rotate_dst;
src = imread( argv[1], IMREAD_COLOR );
warp_dst = Mat::zeros( src.rows, src.cols, src.type() );
srcTri[0] = Point2f( 0,0 );
srcTri[1] = Point2f( src.cols - 1.f, 0 );
srcTri[2] = Point2f( 0, src.rows - 1.f );
dstTri[0] = Point2f( src.cols*0.0f, src.rows*0.33f );
dstTri[1] = Point2f( src.cols*0.85f, src.rows*0.25f );
dstTri[2] = Point2f( src.cols*0.15f, src.rows*0.7f );
warp_mat = getAffineTransform( srcTri, dstTri );
warpAffine( src, warp_dst, warp_mat, warp_dst.size() );
Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );
double angle = -50.0;
double scale = 0.6;
rot_mat = getRotationMatrix2D( center, angle, scale );
warpAffine( warp_dst, warp_rotate_dst, rot_mat, warp_dst.size() );
namedWindow( source_window, WINDOW_AUTOSIZE );
imshow( source_window, src );
namedWindow( warp_window, WINDOW_AUTOSIZE );
imshow( warp_window, warp_dst );
namedWindow( warp_rotate_window, WINDOW_AUTOSIZE );
imshow( warp_rotate_window, warp_rotate_dst );
waitKey(0);
return 0;
}说明
- 声明我们将使用的一些变量,例如存储我们的结果的矩阵和2个点数组,以存储定义我们的Affine变换的2D点。
Point2f srcTri [3];
Point2f dstTri [3];
Mat rot_mat(2,3,CV_32FC1);
Mat warp_mat(2,3,CV_32FC1);
Mat src,warp_dst,warp_rotate_dst;- 加载图片:
src = imread(argv [1],1);
- 将目标图像初始化为具有与源相同的大小和类型:
warp_dst = Mat :: zeros(src.rows,src.cols,src.type());
- 仿射变换:如上所述,我们需要两组3点来推导仿射变换关系。看一看:
srcTri [0] = Point2f(0,0);
srcTri [1] = Point2f(src.cols - 1,0);
srcTri [2] = Point2f(0,src.rows - 1);
dstTri [0] = Point2f(src.cols * 0.0,src.rows * 0.33);
dstTri [1] = Point2f(src.cols * 0.85,src.rows * 0.25);
dstTri [2] = Point2f(src.cols * 0.15,src.rows * 0.7);您可能想要绘制这些要点,以便更好地了解其变化。它们的位置与示例图中所示的位置大致相同(在理论部分)。您可能会注意到由3点定义的三角形的大小和方向改变。
- 使用两组点,我们使用OpenCV函数cv :: getAffineTransform计算Affine Transform :
warp_mat = getAffineTransform(srcTri,dstTri);
我们得到一个2×3矩阵作为输出(在这种情况下为warp_mat)
- 然后我们将刚刚发现的仿射变换应用到src图像
warpAffine(src,warp_dst,warp_mat,warp_dst.size());
具有以下参数:
- src:输入图像
- warp_dst:输出图像
- warp_mat:仿射变换
- warp_dst.size():输出图像所需的大小
我们刚刚得到了我们的第一个转换的形象 我们会显示一下。在此之前,我们也想旋转它...
- 旋转:要旋转图像,我们需要知道两件事情:
- 相对于图像将旋转的中心
- 要旋转的角度。在OpenCV中,正角度是逆时针方向
- 可选:比例因子
我们使用以下代码片段定义这些参数:
Point center = Point( warp_dst.cols/2, warp_dst.rows/2 );
double angle = -50.0;
double scale = 0.6;- 我们用OpenCV函数cv :: getRotationMatrix2D生成旋转矩阵,它返回一个2×3矩阵(在这种情况下为rot_mat)
rot_mat = getRotationMatrix2D( center, angle, scale );
- 我们现在将找到的旋转应用到我们以前的转换的输出。
warpAffine(warp_dst,warp_rotate_dst,rot_mat,warp_dst.size());
- 最后,我们在两个窗口中显示我们的结果,加上原始图像的良好度量:
namedWindow(source_window,WINDOW_AUTOSIZE);
imshow(source_window,src);
namedWindow(warp_window,WINDOW_AUTOSIZE);
imshow(warp_window,warp_dst);
namedWindow(warp_rotate_window,WINDOW_AUTOSIZE);
imshow(warp_rotate_window,warp_rotate_dst);- 我们只需要等到用户退出程序
waitKey(0);
结果
在编译上面的代码之后,我们可以给它一个图像的路径作为参数。例如,对于像:

在应用第一个仿射变换后,我们得到:
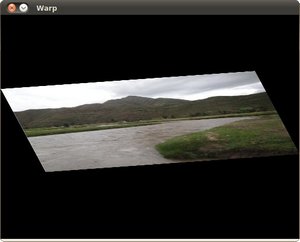
最后,在应用负旋转(记住负方向顺时针)和比例因子后,我们得到: