逻辑回归是监督式分类算法，通过逻辑函数（Sigmoid曲线） 估计概率，衡量因变量（目标类别）与自变量（特征）的关系，适用于二分类或多分类问题。

1. 前置条件

需安装Tkinter包（用于可视化），安装地址：https://docs.python.org/2/library/tkinter.html 。

2. 实现步骤

步骤1：导入库

import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt

步骤2：定义样本数据

## 特征（2个维度）
X = np.array([[2, 4.8], [2.9, 4.7], [2.5, 5], [3.2, 5.5], [6, 5], [7.6, 4],
              [3.2, 0.9], [2.9, 1.9], [2.4, 3.5], [0.5, 3.4], [1, 4], [0.9, 5.9]])
## 标签（4个类别：0、1、2、3）
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3])

步骤3：创建并训练逻辑回归分类器

## 初始化分类器（solver=优化器，C=正则化参数）
classifier_LR = linear_model.LogisticRegression(solver='liblinear', C=75)
## 训练模型
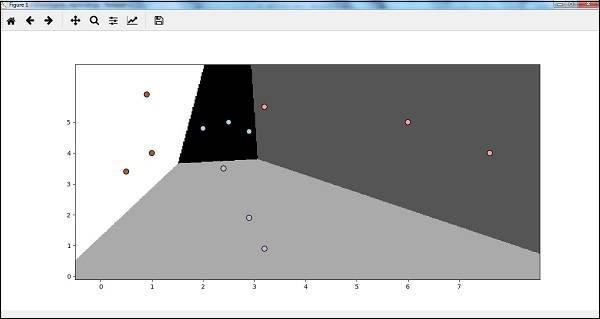
classifier_LR.fit(X, y)

步骤4：模型结果可视化

定义可视化函数，绘制分类边界：

def logistic_visualize(classifier_LR, X, y):
    # 定义网格边界
    min_x, max_x = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
    min_y, max_y = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0
    # 定义网格步长
    mesh_step_size = 0.02
    # 生成网格点
    x_vals, y_vals = np.meshgrid(
        np.arange(min_x, max_x, mesh_step_size),
        np.arange(min_y, max_y, mesh_step_size)
    )
    # 对网格点进行预测
    output = classifier_LR.predict(np.c_[x_vals.ravel(), y_vals.ravel()])
    output = output.reshape(x_vals.shape)
    # 绘制分类边界
    plt.figure()
    plt.pcolormesh(x_vals, y_vals, output, cmap=plt.cm.gray)
    # 绘制原始数据点
    plt.scatter(X[:, 0], X[:, 1], c=y, s=75, edgecolors='black', linewidth=1, cmap=plt.cm.Paired)
    # 设置坐标轴范围与刻度
    plt.xlim(x_vals.min(), x_vals.max())
    plt.ylim(y_vals.min(), y_vals.max())
    plt.xticks(np.arange(int(X[:, 0].min() - 1), int(X[:, 0].max() + 1), 1.0))
    plt.yticks(np.arange(int(X[:, 1].min() - 1), int(X[:, 1].max() + 1), 1.0))
    plt.show()


## 调用可视化函数
logistic_visualize(classifier_LR, X, y)