本节将介绍几种最常见的机器学习算法，具体如下：

线性回归

它是统计学和机器学习领域中最知名的算法之一。

• 核心概念：线性回归是一种线性模型，假设输入变量（设为x）与单一输出变量（设为y）之间存在线性关系。换句话说，y可以通过输入变量x的线性组合计算得出。变量之间的关系可通过拟合一条最佳直线来确立。
• 线性回归的类型：
  1. 简单线性回归：若仅包含一个自变量，则该线性回归算法称为简单线性回归。
  2. 多元线性回归：若包含多个自变量，则该线性回归算法称为多元线性回归。

线性回归主要用于基于连续变量估算实数值。例如，可通过线性回归估算一家店铺一天的总销售额（基于实数值）。

逻辑回归

它是一种分类算法，也被称为对数几率回归。 逻辑回归主要用于基于给定的一组自变量，估算离散值（如0或1、真或假、是或否）。本质上，它预测的是概率，因此输出结果介于0到1之间。

决策树

决策树是一种监督式学习算法，主要用于分类问题。 它本质上是一种基于自变量的递归划分分类器，由节点构成有根树。有根树是一种有向树，包含一个称为根节点的节点，根节点没有入边，其他所有节点均有一条入边。这些节点被称为叶节点或决策节点。例如，以下决策树可用于判断一个人是否健康：

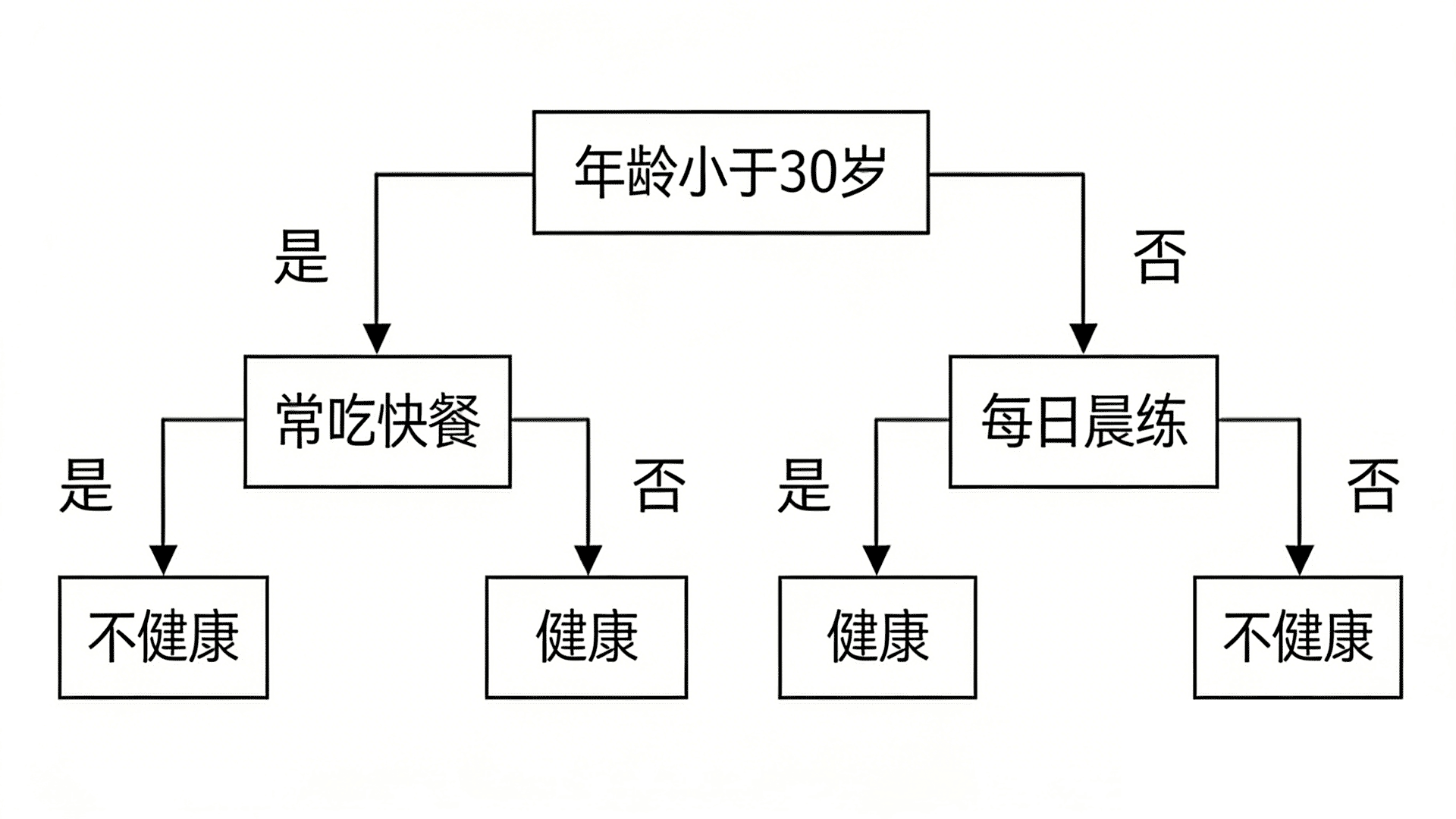
• 年龄<30岁
  • 是 → 常吃快餐
  • 是 → 不健康
  • 否 → 健康
  • 否 → 每天早上锻炼
  • 是 → 健康
  • 否 → 不健康

支持向量机（SVM）

它可用于分类和回归问题，但主要应用于分类问题。 支持向量机的核心概念是：将每个数据项表示为n维空间中的一个点，其中每个特征的值对应一个特定坐标（n为特征数量）。以下是理解支持向量机概念的简单图形示意：

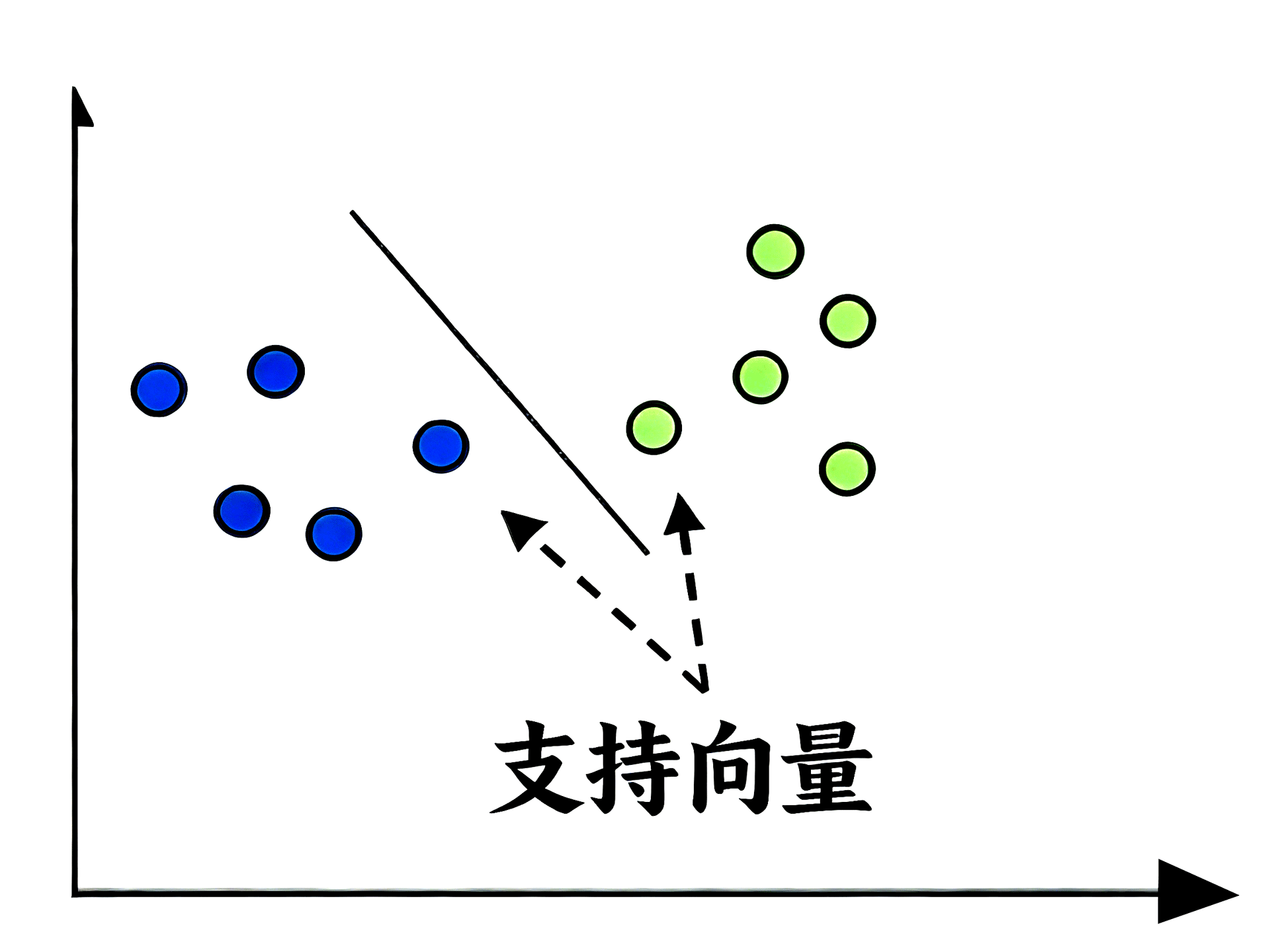
• 支持向量：在上图中，我们有两个特征，因此首先需要将这两个变量绘制在二维空间中，每个点有两个坐标，这些点被称为支持向量。直线将数据划分为两个不同的分类组，这条直线就是分类器。

朴素贝叶斯

它也是一种分类技术，其核心逻辑是利用贝叶斯定理构建分类器，假设各个预测变量相互独立。简单来说，它认为某一类中某个特征的存在与其他任何特征的存在无关。贝叶斯定理的公式如下：

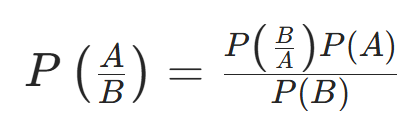
$$P\left ( \frac{A}{B} \right ) = \frac{P\left ( \frac{B}{A} \right )P\left ( A \right )}{P\left ( B \right )}$$

朴素贝叶斯模型易于构建，尤其适用于大型数据集。

K近邻算法（KNN）

它可用于分类和回归问题，广泛应用于解决分类问题。 该算法的核心概念是：存储所有可用样本，通过新样本的k个邻近样本的多数投票来对其进行分类。新样本将被分配给在其k个最近邻中最常见的类别（通过距离函数衡量）。距离函数包括欧几里得距离、明可夫斯基距离和汉明距离。使用K近邻算法时需注意：

• 计算成本高于其他分类算法；
• 需要对变量进行归一化，否则取值范围较大的变量可能会产生偏差；
• 需在预处理阶段进行噪声去除等操作。

K均值聚类

顾名思义，它用于解决聚类问题，本质上是一种无监督式学习算法。 K均值聚类算法的核心逻辑是通过若干个聚类对数据集进行分类。通过以下步骤可利用K均值算法形成聚类：

1. K均值算法为每个聚类选择k个点作为质心；
2. 每个数据点与距离最近的质心形成一个聚类，即形成k个聚类；
3. 基于每个聚类现有的成员，重新计算该聚类的质心；
4. 重复上述步骤，直至收敛。

随机森林

它是一种监督式分类算法，优势在于可同时用于分类和回归问题。 本质上，它是决策树的集合（即“森林”），也可称为决策树集成。随机森林的核心概念是：每棵树都会给出一个分类结果，森林最终选择其中最优的分类结果。随机森林算法的优势如下：

• 可同时用于分类和回归任务；
• 能处理缺失值；
• 即使森林中决策树数量较多，也不会出现模型过拟合的情况。