回归分析是统计学与机器学习中最重要的工具之一，甚至可以说机器学习的入门之旅始于回归。它是一种参数化技术，能够基于数据做出决策，或者通过学习输入变量与输出变量之间的关系，实现基于数据的预测。在回归分析中，依赖于输入变量的输出变量是连续值实数，核心价值在于揭示输入变量变化时，输出变量的变化规律。回归分析常用于价格预测、经济趋势分析、变量变化预测等场景。

一、在Python中构建回归器

本节将详细介绍如何构建单变量回归器和多变量回归器，所有实现均基于Python 3及Scikit-learn库。

（一）线性回归器/单变量回归器

单变量线性回归假设输入变量（单一自变量）与输出变量之间存在线性关系，模型形式为 ( y = wx + b )（( w ) 为权重，( b ) 为偏置）。

1. 实现步骤

步骤1：导入所需库

import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt

步骤2：加载输入数据

假设数据存储在 linear.txt 文件中（每行包含一个自变量和一个因变量，以逗号分隔），使用 np.loadtxt 加载数据：

## 数据文件路径（根据实际情况修改）
input_file = 'D:/ProgramData/linear.txt'
## 加载数据，按逗号分隔
input_data = np.loadtxt(input_file, delimiter=',')
## 划分自变量（X）和因变量（y）
X, y = input_data[:, :-1], input_data[:, -1]

步骤3：划分训练集与测试集

将60%的数据用于模型训练，40%用于测试：

## 训练集样本数（60%）
training_samples = int(0.6 * len(X))
## 测试集样本数
testing_samples = len(X) - training_samples


## 划分训练集和测试集
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]

步骤4：创建并训练线性回归模型

## 初始化线性回归器
reg_linear = linear_model.LinearRegression()
## 用训练集训练模型
reg_linear.fit(X_train, y_train)

步骤5：模型预测

使用训练好的模型对测试集进行预测：

y_test_pred = reg_linear.predict(X_test)

步骤6：结果可视化

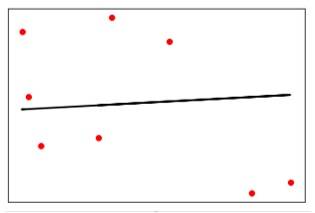
通过散点图展示测试集真实值与模型预测值的对比：

## 绘制测试集真实值（红色散点）
plt.scatter(X_test, y_test, color='red')
## 绘制预测值（黑色直线）
plt.plot(X_test, y_test_pred, color='black', linewidth=2)
## 隐藏坐标轴刻度
plt.xticks(())
plt.yticks(())
## 显示图像
plt.show()

步骤7：模型性能评估

使用多种指标评估回归模型的性能，包括平均绝对误差、均方误差、中位数绝对误差、解释方差得分和决定系数（R² 得分）：

print("线性回归器性能评估：")
print(f"平均绝对误差 = {round(sm.mean_absolute_error(y_test, y_test_pred), 2)}")
print(f"均方误差 = {round(sm.mean_squared_error(y_test, y_test_pred), 2)}")
print(f"中位数绝对误差 = {round(sm.median_absolute_error(y_test, y_test_pred), 2)}")
print(f"解释方差得分 = {round(sm.explained_variance_score(y_test, y_test_pred), 2)}")
print(f"R² 得分 = {round(sm.r2_score(y_test, y_test_pred), 2)}")

2. 输出结果示例

线性回归器性能评估：
平均绝对误差 = 1.78
均方误差 = 3.89
中位数绝对误差 = 2.01
解释方差得分 = -0.09
R² 得分 = -0.09

结果说明：R² 得分为负，表明模型性能较差，可能是由于样本量过小或数据非线性关系导致。实际应用中可使用更大规模的数据集（如通过 sklearn.datasets 导入内置数据集）。

3. 示例数据（linear.txt）

若需测试，可使用以下小型数据集（每行对应一组 (x, y)）：

2,4.8
2.9,4.7
2.5,5
3.2,5.5
6,5
7.6,4
3.2,0.9
2.9,1.9
2.4,3.5
0.5,3.4
1,4
0.9,5.9
1.2,2.58
3.2,5.6
5.1,1.5
4.5,1.2
2.3,6.3
2.1,2.8

（二）多变量回归器

多变量线性回归包含多个自变量，模型形式为 ( y = w_1x_1 + w_2x_2 + ... + w_nx_n + b )，可拟合多个因素共同影响的输出变量。此外，还将介绍多项式回归，用于拟合非线性关系。

1. 实现步骤

步骤1：导入所需库（新增多项式特征处理库）

import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures

步骤2：加载输入数据

数据存储在 Mul_linear.txt 文件中（每行包含多个自变量和一个因变量，以逗号分隔）：

## 数据文件路径（根据实际情况修改）
input_file = 'D:/ProgramData/Mul_linear.txt'
## 加载数据，按逗号分隔
input_data = np.loadtxt(input_file, delimiter=',')
## 划分自变量（X）和因变量（y）
X, y = input_data[:, :-1], input_data[:, -1]

步骤3：划分训练集与测试集

## 训练集样本数（60%）
training_samples = int(0.6 * len(X))
## 测试集样本数
testing_samples = len(X) - training_samples


## 划分训练集和测试集
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]

步骤4：创建并训练多变量线性回归模型

## 初始化多变量线性回归器
reg_linear_mul = linear_model.LinearRegression()
## 用训练集训练模型
reg_linear_mul.fit(X_train, y_train)

步骤5：模型预测与性能评估

## 对测试集进行预测
y_test_pred = reg_linear_mul.predict(X_test)


## 性能评估
print("多变量线性回归器性能评估：")
print(f"平均绝对误差 = {round(sm.mean_absolute_error(y_test, y_test_pred), 2)}")
print(f"均方误差 = {round(sm.mean_squared_error(y_test, y_test_pred), 2)}")
print(f"中位数绝对误差 = {round(sm.median_absolute_error(y_test, y_test_pred), 2)}")
print(f"解释方差得分 = {round(sm.explained_variance_score(y_test, y_test_pred), 2)}")
print(f"R² 得分 = {round(sm.r2_score(y_test, y_test_pred), 2)}")

步骤6：多项式回归（拟合非线性关系）

当数据呈现非线性关系时，可使用多项式回归（此处以10次多项式为例）：

## 构建10次多项式特征
polynomial = PolynomialFeatures(degree=10)
## 转换训练集特征（将线性特征转换为多项式特征）
X_train_transformed = polynomial.fit_transform(X_train)


## 定义一个测试数据点（包含3个自变量）
datapoint = [[2.23, 1.35, 1.12]]
## 转换测试数据点的特征
poly_datapoint = polynomial.fit_transform(datapoint)


## 初始化多项式回归模型
poly_linear_model = linear_model.LinearRegression()
## 训练多项式回归模型
poly_linear_model.fit(X_train_transformed, y_train)


## 对比线性回归与多项式回归的预测结果
print("\n线性回归预测结果：")
print(reg_linear_mul.predict(datapoint))
print("\n多项式回归预测结果：")
print(poly_linear_model.predict(poly_datapoint))

2. 输出结果示例

多变量线性回归器性能评估：
平均绝对误差 = 0.6
均方误差 = 0.65
中位数绝对误差 = 0.41
解释方差得分 = 0.34
R² 得分 = 0.33


线性回归预测结果：
[2.40170462]


多项式回归预测结果：
[1.8697225]

3. 示例数据（Mul_linear.txt）

以下是包含3个自变量和1个因变量的示例数据：

2,4.8,1.2,3.2
2.9,4.7,1.5,3.6
2.5,5,2.8,2
3.2,5.5,3.5,2.1
6,5,2,3.2
7.6,4,1.2,3.2
3.2,0.9,2.3,1.4
2.9,1.9,2.3,1.2
2.4,3.5,2.8,3.6
0.5,3.4,1.8,2.9
1,4,3,2.5
0.9,5.9,5.6,0.8
1.2,2.58,3.45,1.23
3.2,5.6,2,3.2
5.1,1.5,1.2,1.3
4.5,1.2,4.1,2.3
2.3,6.3,2.5,3.2
2.1,2.8,1.2,3.6

二、关键说明

1. 数据格式：回归分析要求输入数据为数值型，若存在分类变量，需先进行编码（如标签编码、独热编码）。
2. 模型选择：
   • 线性回归适用于变量间呈线性关系的场景；
   • 多项式回归适用于非线性关系，但需注意过度拟合（可通过调整多项式次数或使用正则化缓解）。
3. 性能指标：
   • R² 得分越接近1，表明模型拟合效果越好；
   • 均方误差（MSE）对异常值敏感，若数据存在异常值，可优先使用中位数绝对误差。
4. 扩展应用：实际场景中可使用更大规模的数据集（如 sklearn.datasets.load_diabetes 糖尿病数据集），或通过特征工程优化模型性能。