现实世界中的数据并非天然会划分为多个边界清晰的簇，因此难以直接通过可视化来推断聚类效果，这就需要我们对聚类的性能和质量进行量化评估，轮廓分析是实现这一目标的常用方法。

（一）轮廓分析（Silhouette Analysis）

该方法通过衡量簇与簇之间的距离来检验聚类质量，还能为簇数这类参数的选择提供依据——核心指标为轮廓系数（silhouette score）。

轮廓系数用于量化评估数据集中每个点与所属簇的贴合程度，以及与相邻簇的分离程度，是判断聚类效果的核心指标。

（二）轮廓系数结果分析

轮廓系数的取值范围为[-1, 1]，不同取值对应不同的聚类效果，具体分析如下：

• 系数接近+1：表示该数据点远离相邻簇，与所属簇的贴合度极高，聚类效果优秀；
• 系数接近0：表示该数据点位于两个相邻簇的决策边界上（或极近），聚类划分模糊；
• 系数为-1：表示该数据点被错误分配至簇中，聚类效果极差。

（三）轮廓系数计算公式

轮廓系数的计算公式如下：

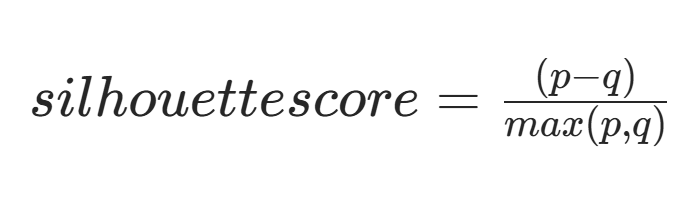
$$silhouette score = \frac{\left ( p-q \right )}{max\left ( p,q \right )}$$

其中：

• $q$：该数据点到所属簇内所有其他点的平均距离（簇内平均距离）；
• $p$：该数据点到最近的相邻簇内所有点的平均距离（簇间最小平均距离）。

（四）基于轮廓分析确定最优簇数

以K-Means算法为例，我们可以通过轮廓分析遍历不同的簇数，找到使聚类效果最优的簇数，实现代码如下：

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.datasets.samples_generator import make_blobs


## 生成二维数据集，包含4个数据簇，样本量500
X, y_true = make_blobs(n_samples=500, centers=4, cluster_std=0.40, random_state=0)


## 初始化变量，存储不同簇数对应的轮廓系数
scores = []
## 遍历簇数范围：2~9
values = np.arange(2, 10)


## 迭代训练K-Means模型，计算不同簇数的轮廓系数
for num_clusters in values:
    # 初始化KMeans模型，使用k-means++初始化质心，避免随机初始化的弊端
    kmeans = KMeans(init='k-means++', n_clusters=num_clusters, n_init=10)
    kmeans.fit(X)
    # 计算轮廓系数，使用欧氏距离作为度量
    score = silhouette_score(X, kmeans.labels_, metric='euclidean', sample_size=len(X))
    # 打印簇数与对应轮廓系数
    print("\nNumber of clusters =", num_clusters)
    print("Silhouette score =", score)
    scores.append(score)


## 找到最优簇数（轮廓系数最大对应的簇数）
num_clusters = np.argmax(scores) + values[0]
print('\nOptimal number of clusters =', num_clusters)

代码输出示例：

Number of clusters = 2
Silhouette score = 0.8015503855154122


Number of clusters = 3
Silhouette score = 0.6270122012432992


Number of clusters = 4
Silhouette score = 0.8420423256442592


Number of clusters = 5
Silhouette score = 0.7288580012803229


...


Optimal number of clusters = 4