以下介绍几种最常用的聚类算法，均为无监督学习中实现数据聚类的核心方法。

（一）K-Means算法

K-Means聚类算法是最知名的聚类算法之一，该算法要求预先指定簇的数量，也被称为扁平聚类，是一种迭代式的聚类算法。

实现K-Means算法需遵循以下步骤：

1. 设定所需划分的簇的数量K；
2. 固定簇的数量后，将每个数据点随机分配至某个簇中（即根据簇数对数据做初步分类），并计算每个簇的质心；
3. 由于算法具有迭代性，需要不断更新K个质心的位置，直至找到全局最优解（或质心移动至最优位置，不再发生明显变化）。

Python实现K-Means聚类算法

以下基于Python的Scikit-learn库实现K-Means算法，代码包含数据生成、模型训练与聚类结果可视化：

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets.samples_generator import make_blobs


## 生成二维数据集，包含4个数据簇，样本量500
X, y_true = make_blobs(n_samples=500, centers=4, cluster_std=0.40, random_state=0)


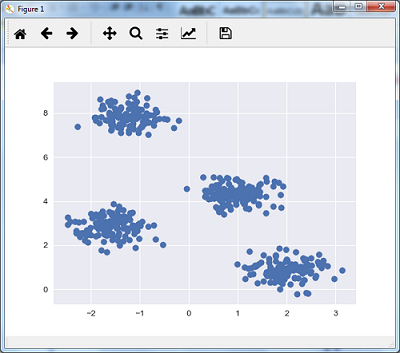
## 可视化原始数据集
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show()


## 初始化KMeans模型，指定簇数为4
kmeans = KMeans(n_clusters=4)
## 用输入数据训练模型
kmeans.fit(X)
## 对数据做聚类预测
y_kmeans = kmeans.predict(X)


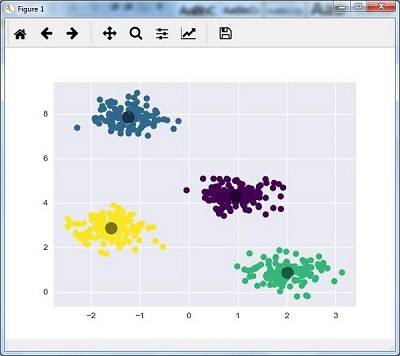
## 可视化聚类结果，不同簇用不同颜色区分
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
## 提取并绘制各簇的质心，黑色实心点表示
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5)
plt.show()

（二）均值漂移算法（Mean Shift Algorithm）

均值漂移算法是另一种流行且高效的无监督聚类算法，该算法无需任何先验假设，属于非参数算法，也被称为层次聚类或均值漂移聚类分析。

实现均值漂移算法的核心步骤：

1. 初始化：将每个数据点视为一个独立的簇；
2. 计算每个簇的质心，并更新新质心的位置；
3. 重复上述步骤，使质心不断向簇的峰值区域移动（即数据密度更高的区域）；
4. 当质心不再发生移动时，算法停止迭代。

Python实现均值漂移聚类算法

以下基于Python的Scikit-learn库实现均值漂移算法，代码包含数据生成、模型训练、聚类结果可视化与簇数估计：

import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.datasets.samples_generator import make_blobs


## 设定簇的质心，生成二维数据集，样本量500
centers = [[2,2], [4,5], [3,10]]
X, _ = make_blobs(n_samples=500, centers=centers, cluster_std=1)


## 可视化原始数据集
plt.scatter(X[:, 0], X[:, 1])
plt.show()


## 初始化并训练均值漂移模型
ms = MeanShift()
ms.fit(X)
## 获取聚类标签与最终质心
labels = ms.labels_
cluster_centers = ms.cluster_centers_


## 打印聚类质心与估计的簇数
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)


## 可视化聚类结果
colors = 10 * ['r.', 'g.', 'b.', 'c.', 'k.', 'y.', 'm.']
for i in range(len(X)):
    plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize=10)
## 绘制聚类质心，黑色叉号表示
plt.scatter(cluster_centers[:,0], cluster_centers[:,1],
            marker="x", color='k', s=150, linewidths=5, zorder=10)
plt.show()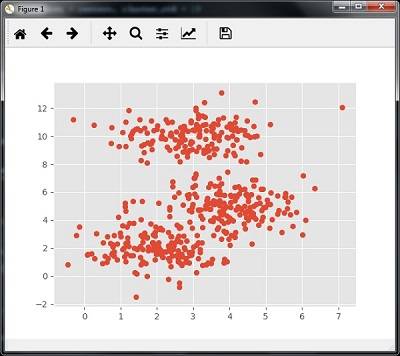

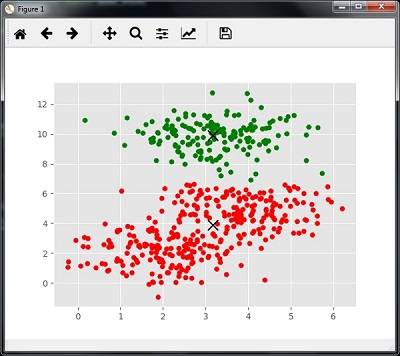
代码输出示例：

[[3.23005036 3.84771893]
 [3.02057451 9.88928991]]
Estimated clusters: 2