全排列问题是回溯算法的一个典型应用。它的定义是在给定一个集合（如一个数组或字符串）的情况下，找出这个集合中元素的所有可能的排列。

表 13-2 列举了几个示例数据，包括输入数组和对应的所有排列。

表 13-2   数组与链表的效率对比

无相等元素的情况

从回溯算法的角度看，我们可以把生成排列的过程想象成一系列选择的结果。假设输入数组为 $[1,2,3]$ ，如果我们先选择 $1$、再选择 $3$、最后选择 $2$ ，则获得排列 $[1,3,2]$ 。回退表示撤销一个选择，之后继续尝试其他选择。

从回溯代码的角度看，候选集合 choices 是输入数组中的所有元素，状态 state 是直至目前已被选择的元素。请注意，每个元素只允许被选择一次，因此 state 中的所有元素都应该是唯一的。

如图 13-5 所示，我们可以将搜索过程展开成一个递归树，树中的每个节点代表当前状态 state 。从根节点开始，经过三轮选择后到达叶节点，每个叶节点都对应一个排列。

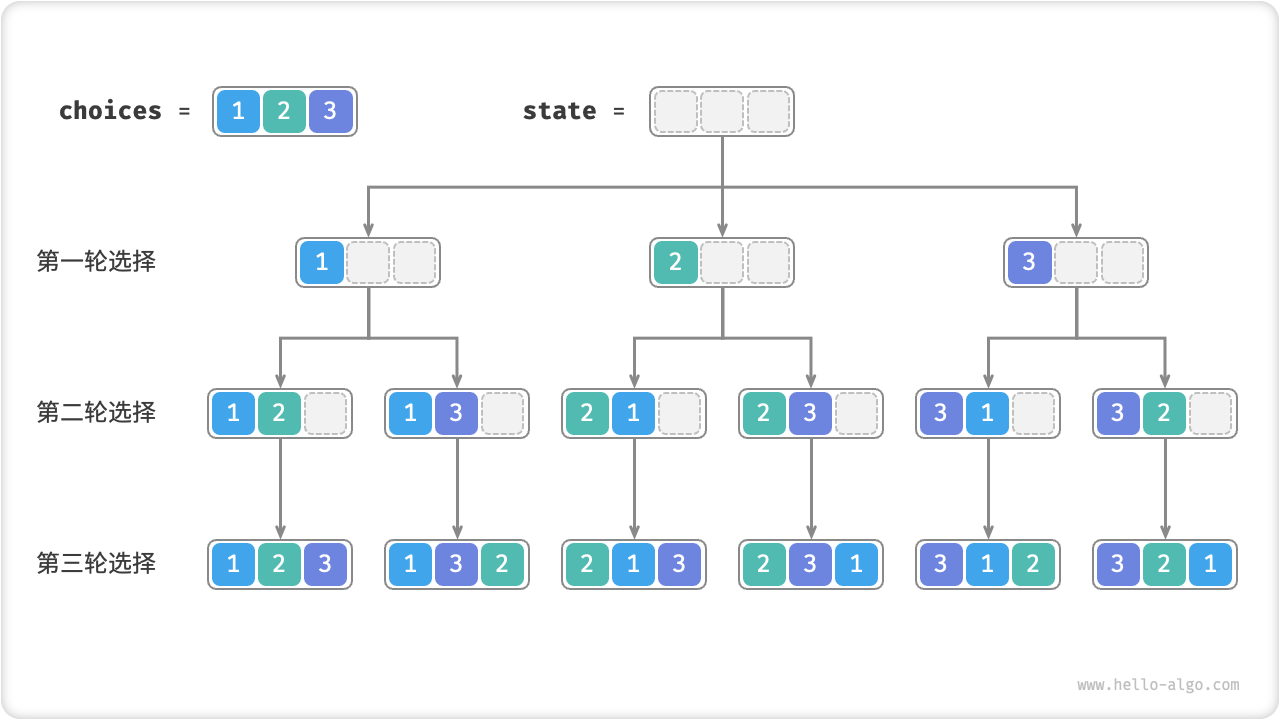
图 13-5   全排列的递归树

1.   重复选择剪枝

为了实现每个元素只被选择一次，我们考虑引入一个布尔型数组 selected ，其中 selected[i] 表示 choices[i] 是否已被选择，并基于它实现以下剪枝操作。

• 在做出选择 choice[i] 后，我们就将 selected[i] 赋值为 $\text{True}$ ，代表它已被选择。
• 遍历选择列表 choices 时，跳过所有已被选择过的节点，即剪枝。

如图 13-6 所示，假设我们第一轮选择 1 ，第二轮选择 3 ，第三轮选择 2 ，则需要在第二轮剪掉元素 1 的分支，在第三轮剪掉元素 1 和元素 3 的分支。

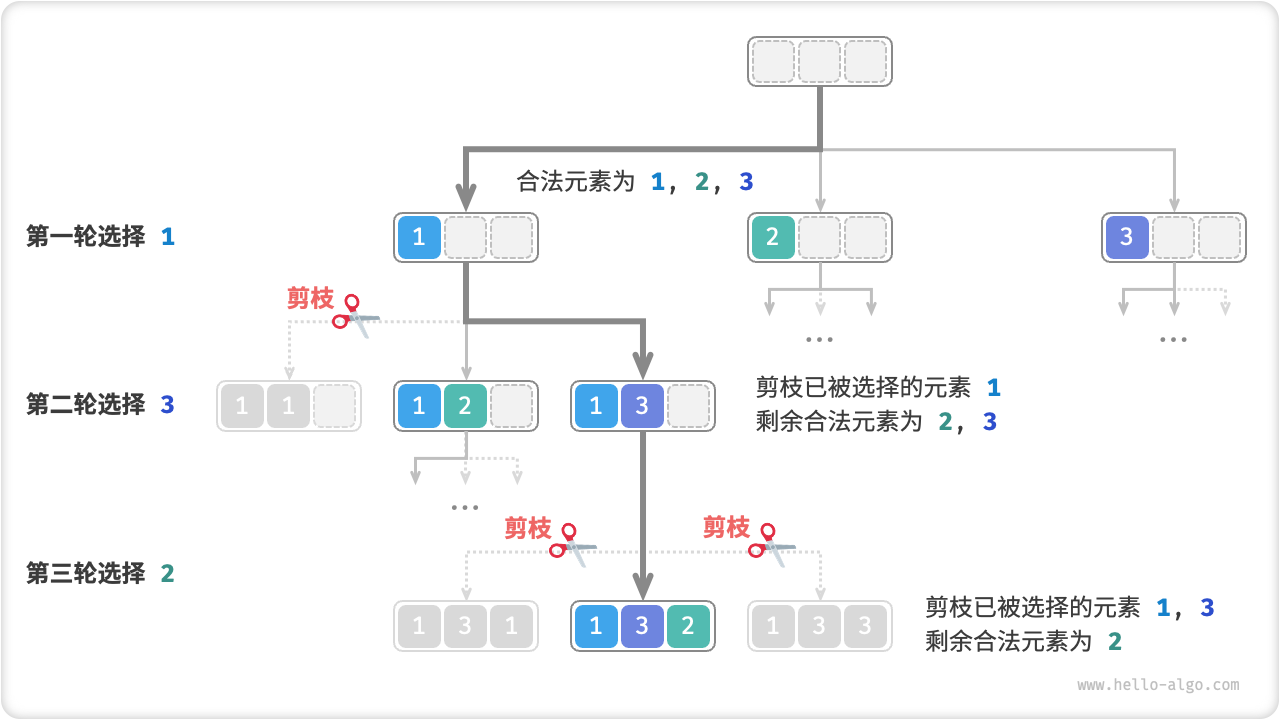
图 13-6   全排列剪枝示例

观察图 13-6 发现，该剪枝操作将搜索空间大小从 $O(n^n)$ 降低至 $O(n!)$ 。

2.   代码实现

想清楚以上信息之后，我们就可以在框架代码中做“完形填空”了。为了缩短代码行数，我们不单独实现框架代码中的各个函数，而是将他们展开在 backtrack() 函数中。

permutations_i.cpp

/* 回溯算法：全排列 I */
void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>> &res) {
    // 当状态长度等于元素数量时，记录解
    if (state.size() == choices.size()) {
        res.push_back(state);
        return;
    }
    // 遍历所有选择
    for (int i = 0; i < choices.size(); i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i]) {
            // 尝试：做出选择，更新状态
            selected[i] = true;
            state.push_back(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop_back();
        }
    }
}

/* 全排列 I */
vector<vector<int>> permutationsI(vector<int> nums) {
    vector<int> state;
    vector<bool> selected(nums.size(), false);
    vector<vector<int>> res;
    backtrack(state, nums, selected, res);
    return res;
}

考虑相等元素的情况

假设输入数组为 $[1,1,2]$ 。为了方便区分两个重复元素 $1$ ，我们将第二个 $1$ 记为 $\hat{1}$ 。

如图 13-7 所示，上述方法生成的排列有一半都是重复的。

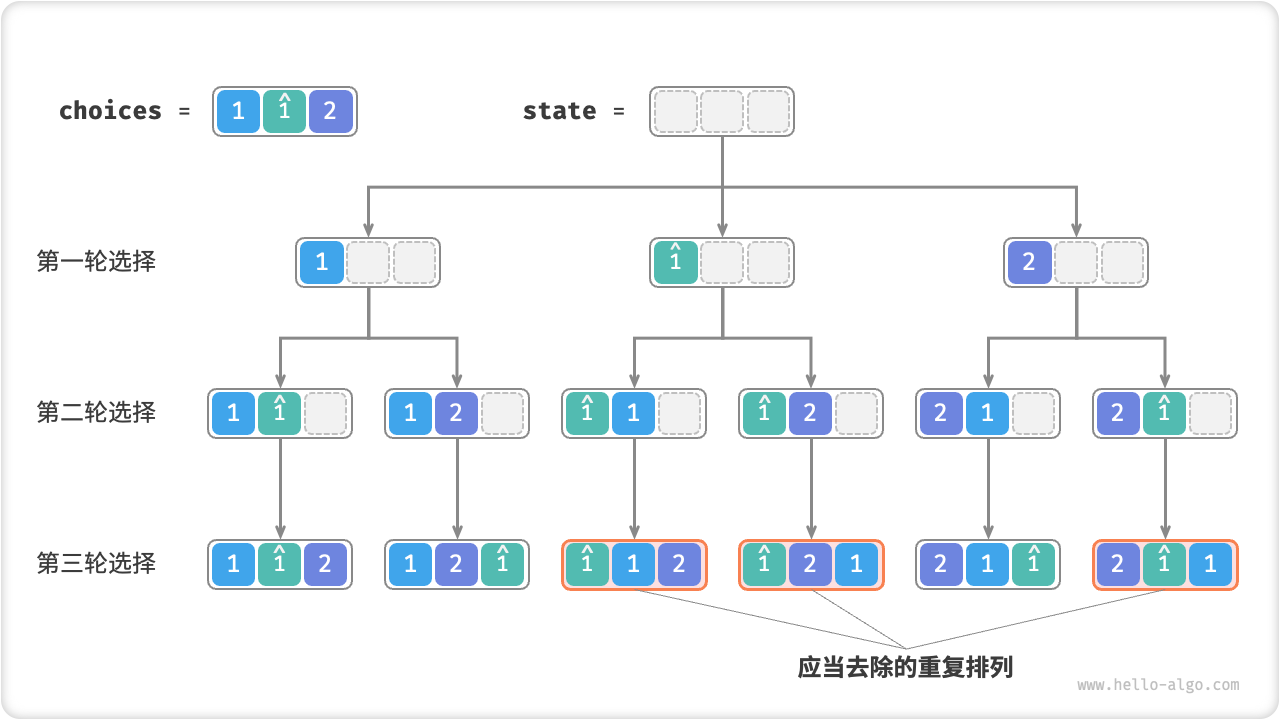
图 13-7   重复排列

那么如何去除重复的排列呢？最直接地，考虑借助一个哈希表，直接对排列结果进行去重。然而这样做不够优雅，因为生成重复排列的搜索分支是没有必要的，应当被提前识别并剪枝，这样可以进一步提升算法效率。

1.   相等元素剪枝¶

观察图 13-8 ，在第一轮中，选择 $1$ 或选择 $\hat{1}$ 是等价的，在这两个选择之下生成的所有排列都是重复的。因此应该把 $\hat{1}$ 剪枝掉。

同理，在第一轮选择 $2$ 之后，第二轮选择中的 $1$ 和 $\hat{1}$ 也会产生重复分支，因此也应将第二轮的 $\hat{1}$ 剪枝。

本质上看，我们的目标是在某一轮选择中，保证多个相等的元素仅被选择一次。

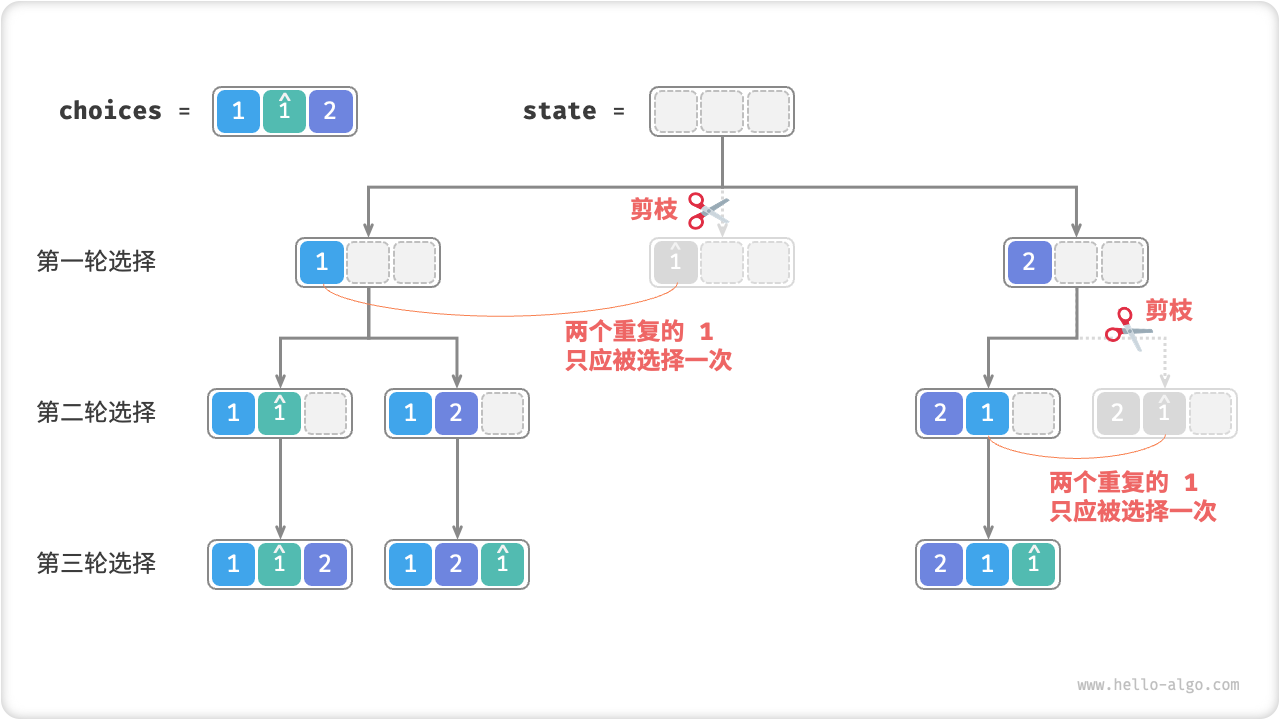
图 13-8   重复排列剪枝

2.   代码实现

在上一题的代码的基础上，我们考虑在每一轮选择中开启一个哈希表 duplicated ，用于记录该轮中已经尝试过的元素，并将重复元素剪枝。

permutations_ii.cpp

/* 回溯算法：全排列 II */
void backtrack(vector<int> &state, const vector<int> &choices, vector<bool> &selected, vector<vector<int>> &res) {
    // 当状态长度等于元素数量时，记录解
    if (state.size() == choices.size()) {
        res.push_back(state);
        return;
    }
    // 遍历所有选择
    unordered_set<int> duplicated;
    for (int i = 0; i < choices.size(); i++) {
        int choice = choices[i];
        // 剪枝：不允许重复选择元素 且 不允许重复选择相等元素
        if (!selected[i] && duplicated.find(choice) == duplicated.end()) {
            // 尝试：做出选择，更新状态
            duplicated.emplace(choice); // 记录选择过的元素值
            selected[i] = true;
            state.push_back(choice);
            // 进行下一轮选择
            backtrack(state, choices, selected, res);
            // 回退：撤销选择，恢复到之前的状态
            selected[i] = false;
            state.pop_back();
        }
    }
}

/* 全排列 II */
vector<vector<int>> permutationsII(vector<int> nums) {
    vector<int> state;
    vector<bool> selected(nums.size(), false);
    vector<vector<int>> res;
    backtrack(state, nums, selected, res);
    return res;
}

假设元素两两之间互不相同，则 $n$ 个元素共有 $n!$ 种排列（阶乘）；在记录结果时，需要复制长度为 $n$ 的列表，使用 $O(n)$ 时间。因此时间复杂度为 $O(n!n)$ 。

最大递归深度为 $n$ ，使用 $O(n)$ 栈帧空间。selected 使用 $O(n)$ 空间。同一时刻最多共有 $n$ 个 duplicated ，使用 $O(n^2)$ 空间。因此空间复杂度为 $O(n^2)$ 。

3.   两种剪枝对比

请注意，虽然 selected 和 duplicated 都用作剪枝，但两者的目标是不同的。

• 重复选择剪枝：整个搜索过程中只有一个 selected 。它记录的是当前状态中包含哪些元素，作用是避免某个元素在 state 中重复出现。
• 相等元素剪枝：每轮选择（即每个开启的 backtrack 函数）都包含一个 duplicated 。它记录的是在遍历中哪些元素已被选择过，作用是保证相等元素只被选择一次。

图 13-9 展示了两个剪枝条件的生效范围。注意，树中的每个节点代表一个选择，从根节点到叶节点的路径上的各个节点构成一个排列。

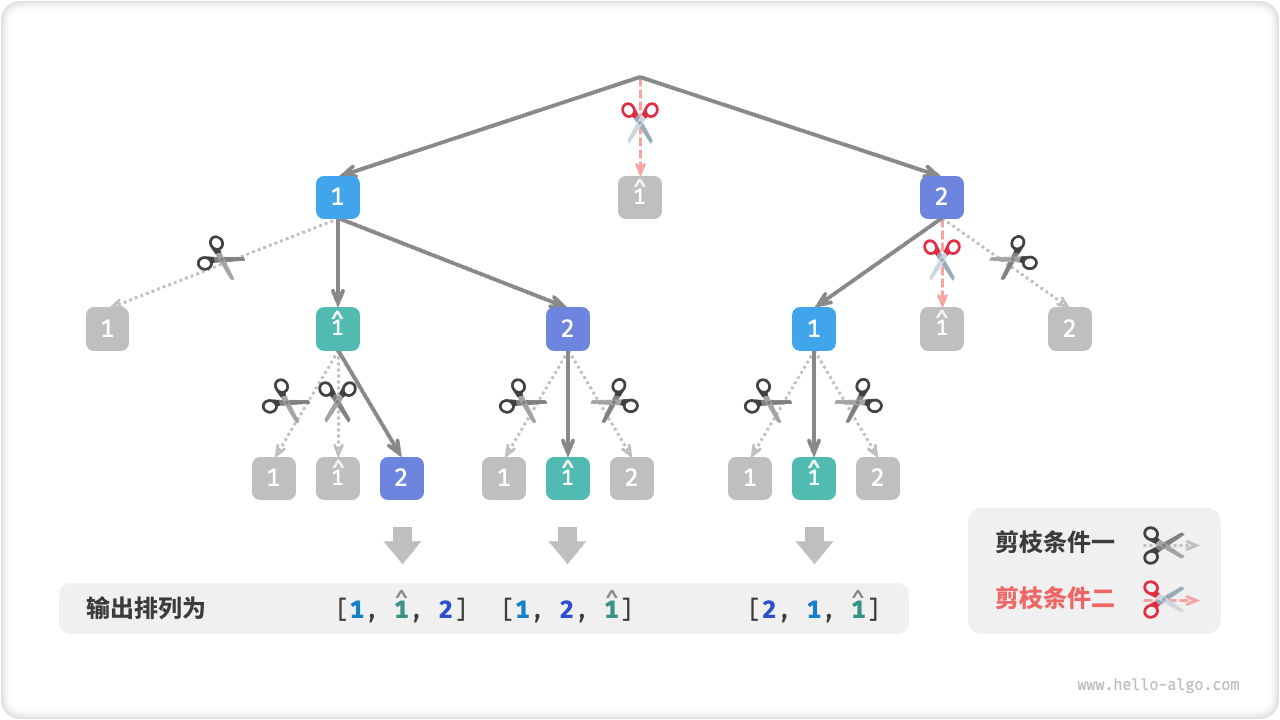
图 13-9   两种剪枝条件的作用范围