
图
「图 graph」是一种非线性数据结构,由「顶点 vertex」和「边 edge」组成。我们可以将图 G 抽象地表示为一组顶点 V 和一组边 E 的集合。以下示例展示了一个包含 5 个顶点和 7 条边的图。
如果将顶点看作节点,将边看作连接各个节点的引用(指针),我们就可以将图看作是一种从链表拓展而来的数据结构。如图 9-1 所示,相较于线性关系(链表)和分治关系(树),网络关系(图)的自由度更高,从而更为复杂。
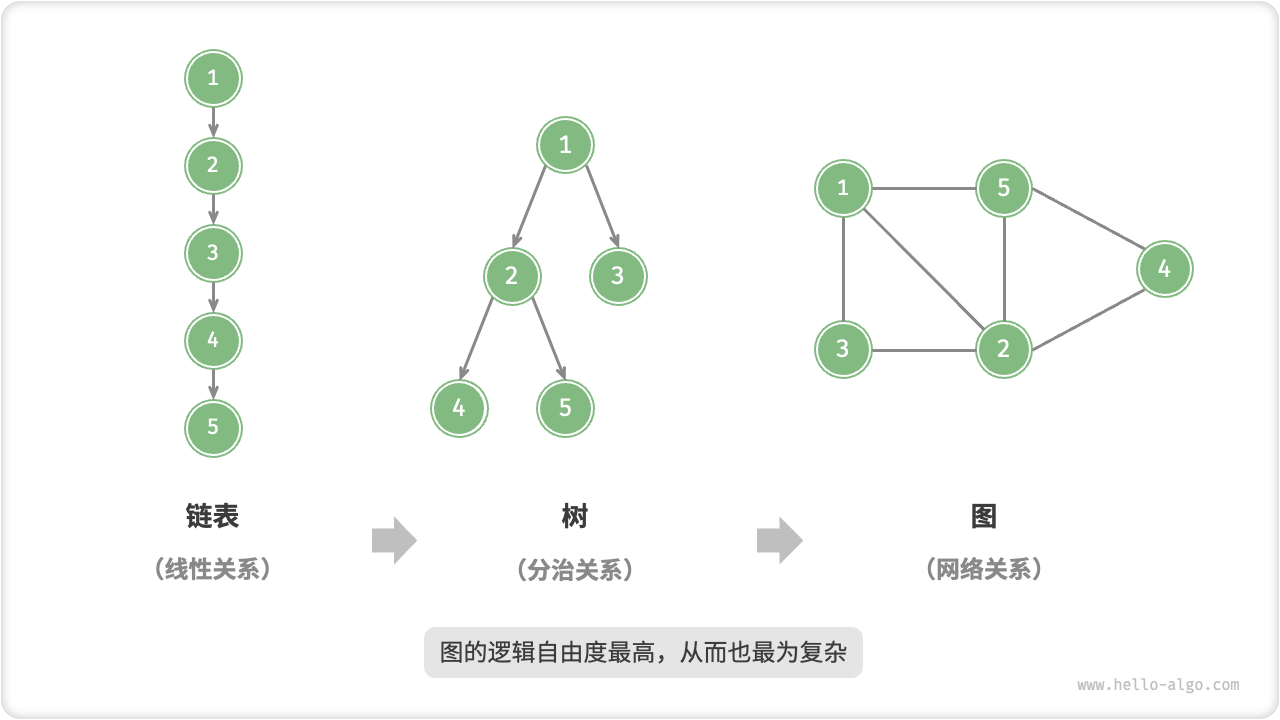
图 9-1 链表、树、图之间的关系
9.1.1 图常见类型与术语
根据边是否具有方向,可分为图 9-2 所示的「无向图 undirected graph」和「有向图 directed graph」。
- 在无向图中,边表示两顶点之间的“双向”连接关系,例如微信或 QQ 中的“好友关系”。
- 在有向图中,边具有方向性,即 A→B 和 A←B 两个方向的边是相互独立的,例如微博或抖音上的“关注”与“被关注”关系。
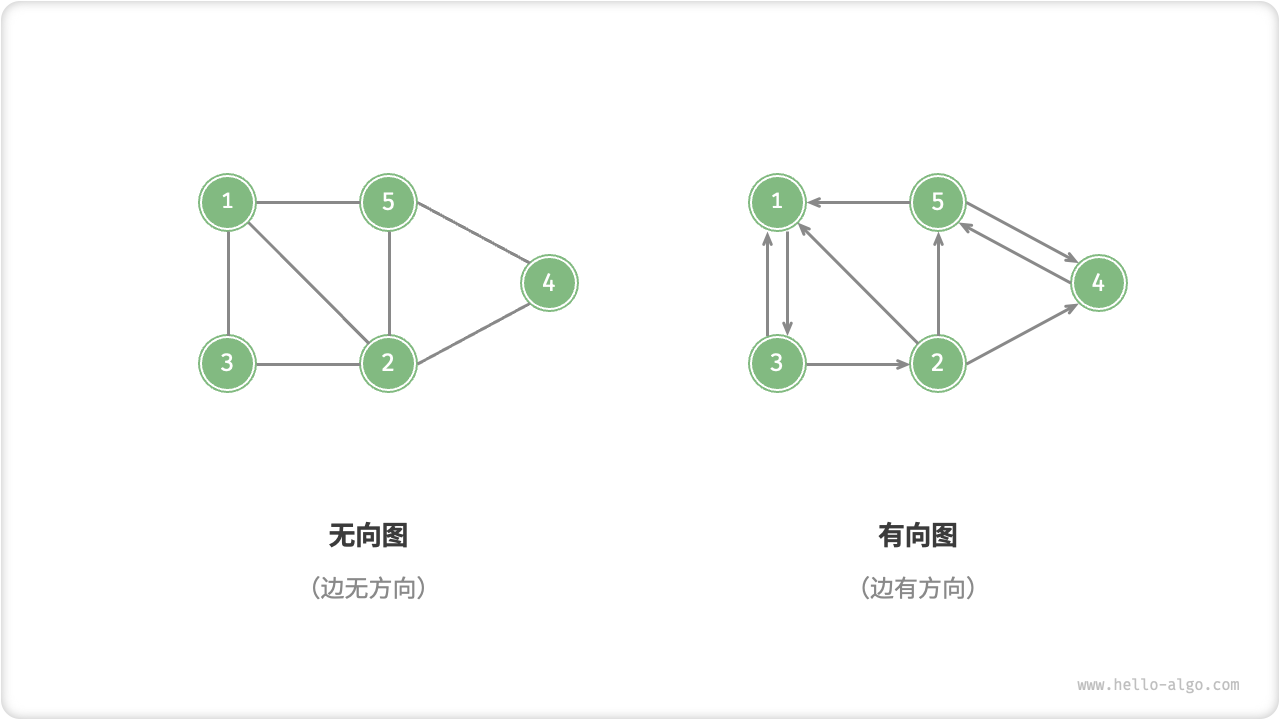
图 9-2 有向图与无向图
根据所有顶点是否连通,可分为图 9-3 所示的「连通图 connected graph」和「非连通图 disconnected graph」。
- 对于连通图,从某个顶点出发,可以到达其余任意顶点。
- 对于非连通图,从某个顶点出发,至少有一个顶点无法到达。
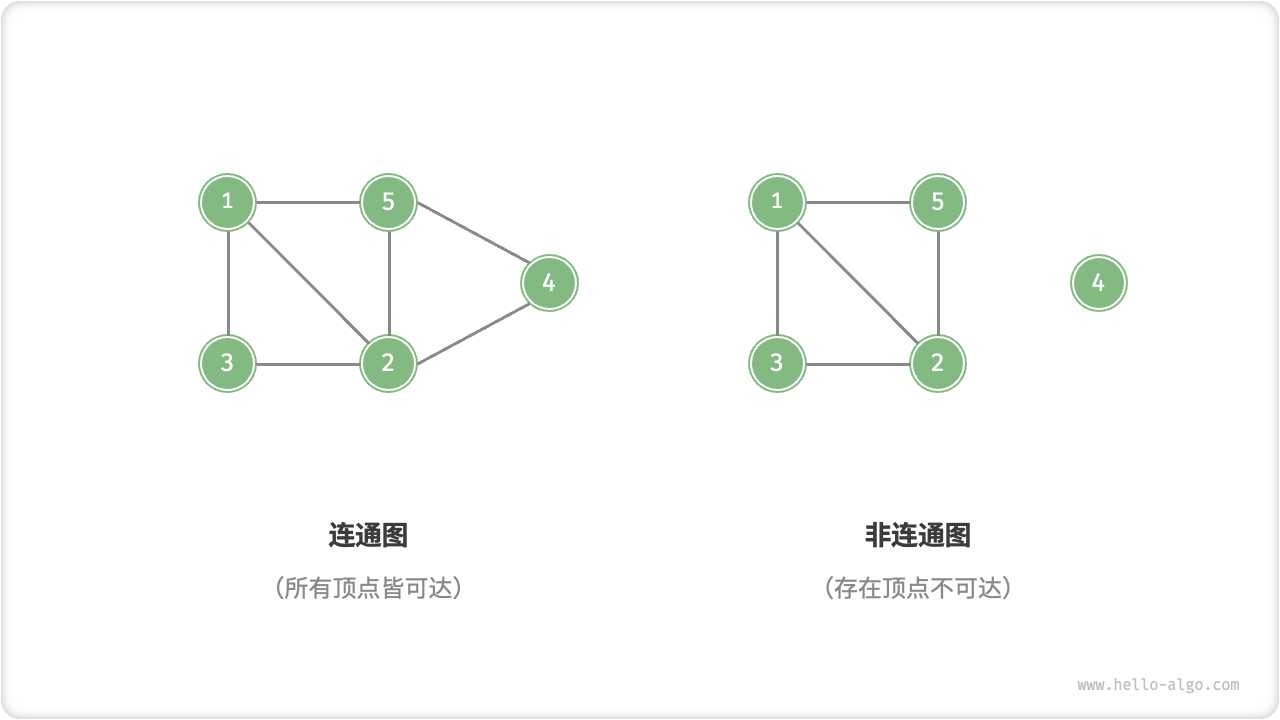
图 9-3 连通图与非连通图
我们还可以为边添加“权重”变量,从而得到图 9-4 所示的「有权图 weighted graph」。例如在王者荣耀等手游中,系统会根据共同游戏时间来计算玩家之间的“亲密度”,这种亲密度网络就可以用有权图来表示。
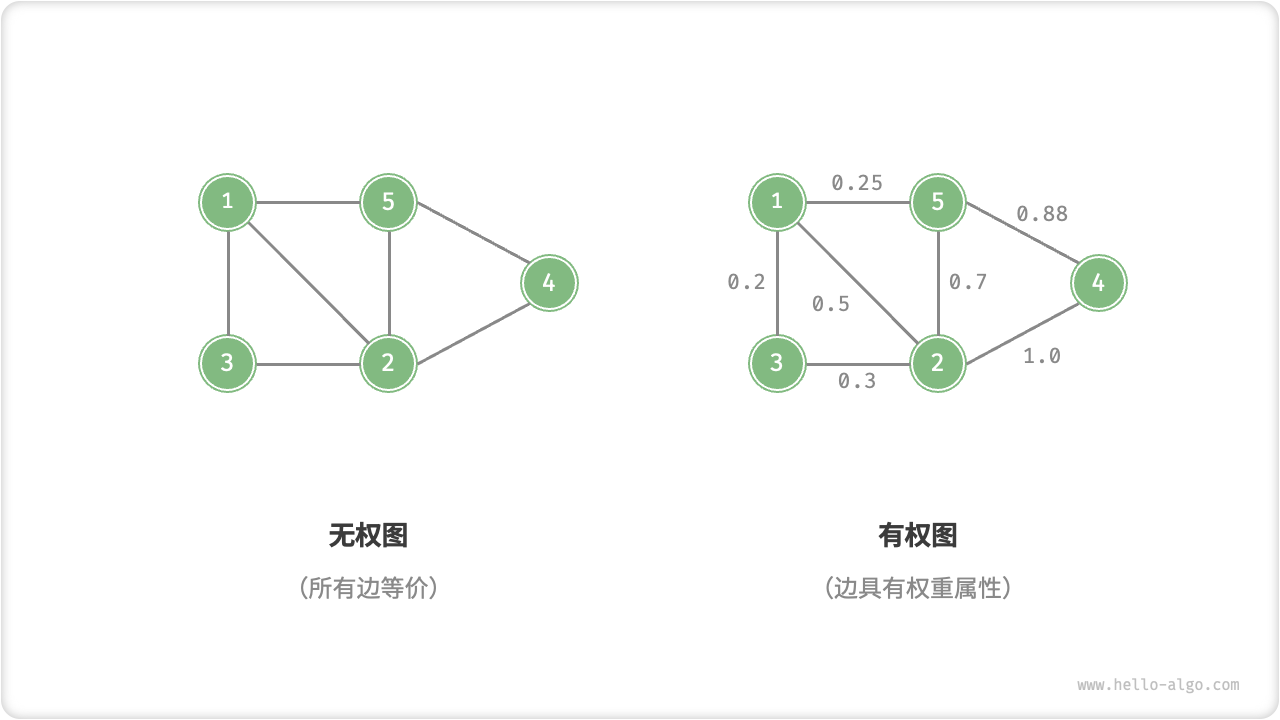
图 9-4 有权图与无权图
图数据结构包含以下常用术语。
- 「邻接 adjacency」:当两顶点之间存在边相连时,称这两顶点“邻接”。在图 9-4 中,顶点 1 的邻接顶点为顶点 2、3、5。
- 「路径 path」:从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”。在图 9-4 中,边序列 1-5-2-4 是顶点 1 到顶点 4 的一条路径。
- 「度 degree」:一个顶点拥有的边数。对于有向图,「入度 In-Degree」表示有多少条边指向该顶点,「出度 Out-Degree」表示有多少条边从该顶点指出。
9.1.2 图的表示
图的常用表示方式包括“邻接矩阵”和“邻接表”。以下使用无向图进行举例。
1. 邻接矩阵
设图的顶点数量为 n ,「邻接矩阵 adjacency matrix」使用一个 n×n 大小的矩阵来表示图,每一行(列)代表一个顶点,矩阵元素代表边,用 1 或 0 表示两个顶点之间是否存在边。
如图 9-5 所示,设邻接矩阵为 M、顶点列表为 V ,那么矩阵元素 M[i,j]=1 表示顶点 V[i] 到顶点 V[j] 之间存在边,反之 M[i,j]=0 表示两顶点之间无边。
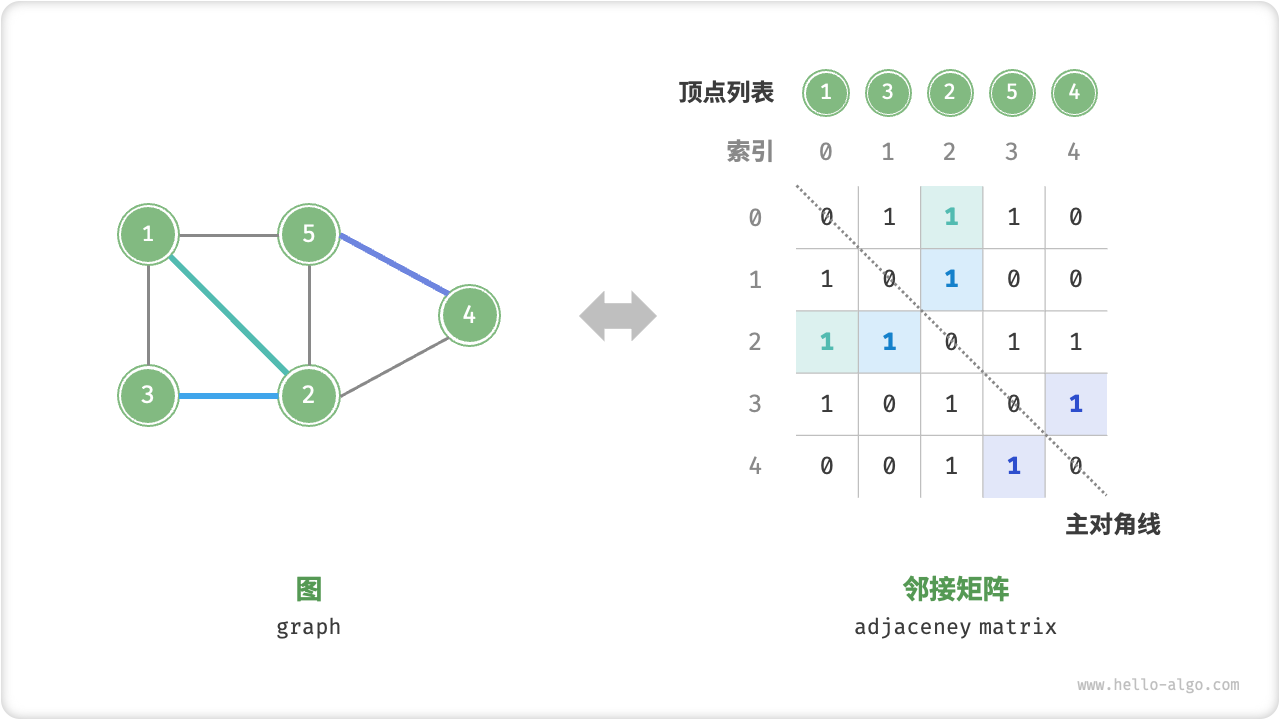
图 9-5 图的邻接矩阵表示
邻接矩阵具有以下特性。
- 顶点不能与自身相连,因此邻接矩阵主对角线元素没有意义。
- 对于无向图,两个方向的边等价,此时邻接矩阵关于主对角线对称。
- 将邻接矩阵的元素从 1 和 0 替换为权重,则可表示有权图。
使用邻接矩阵表示图时,我们可以直接访问矩阵元素以获取边,因此增删查操作的效率很高,时间复杂度均为 O(1) 。然而,矩阵的空间复杂度为 O(n²) ,内存占用较多。
2. 邻接表
「邻接表 adjacency list」使用 n 个链表来表示图,链表节点表示顶点。第 i 条链表对应顶点 i ,其中存储了该顶点的所有邻接顶点(即与该顶点相连的顶点)。图 9-6 展示了一个使用邻接表存储的图的示例。

图 9-6 图的邻接表表示
邻接表仅存储实际存在的边,而边的总数通常远小于 n² ,因此它更加节省空间。然而,在邻接表中需要通过遍历链表来查找边,因此其时间效率不如邻接矩阵。
观察图 9-6 ,邻接表结构与哈希表中的“链式地址”非常相似,因此我们也可以采用类似方法来优化效率。比如当链表较长时,可以将链表转化为 AVL 树或红黑树,从而将时间效率从 O(n) 优化至 O(logn) ;还可以把链表转换为哈希表,从而将时间复杂度降低至 O(1) 。
9.1.3 图常见应用
如表 9-1 所示,许多现实系统都可以用图来建模,相应的问题也可以约化为图计算问题。
表 9-1 现实生活中常见的图
| 顶点 | 边 | 图计算问题 | |
|---|---|---|---|
| 社交网络 | 用户 | 好友关系 | 潜在好友推荐 |
| 地铁线路 | 站点 | 站点间的连通性 | 最短路线推荐 |
| 太阳系 | 星体 | 星体间的万有引力作用 | 行星轨道计算 |