
C++最大切分乘积问题
Question
给定一个正整数
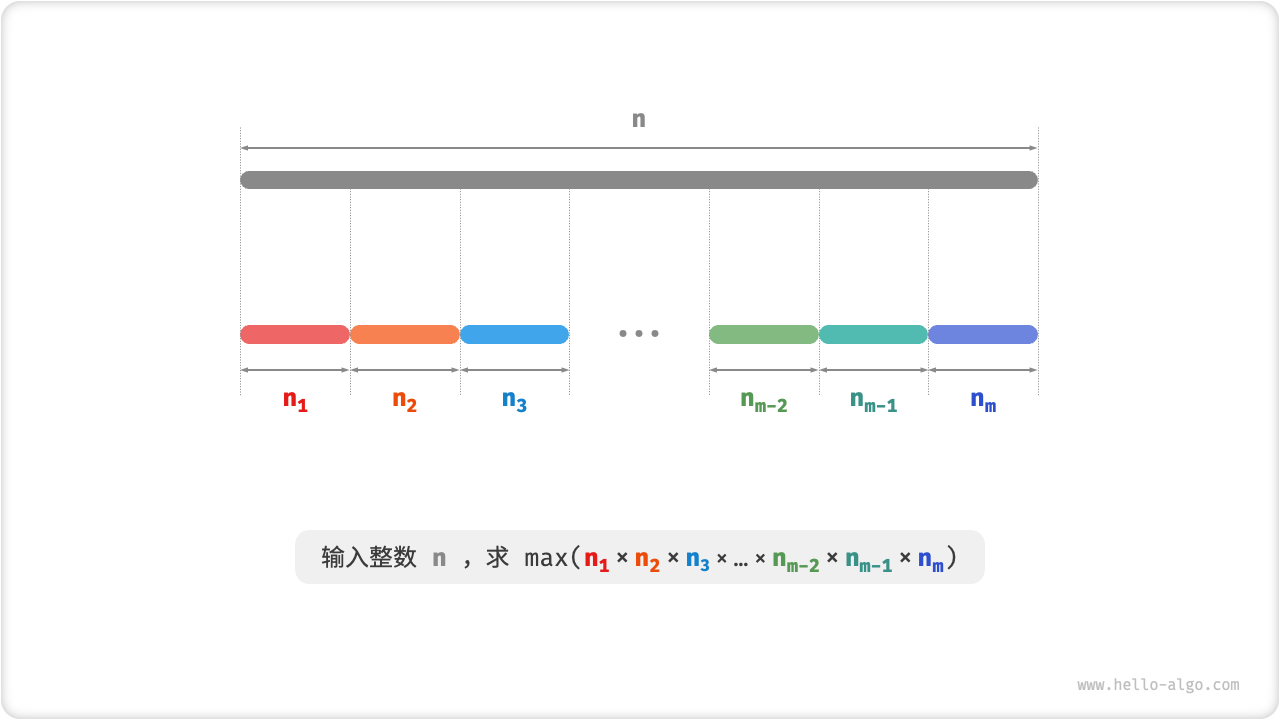
图 15-13 最大切分乘积的问题定义
假设我们将
本题目标是求得所有整数因子的最大乘积,即
我们需要思考的是:切分数量
1. 贪心策略确定
根据经验,两个整数的乘积往往比它们的加和更大。假设从
如图 15-14 所示,当
贪心策略一:如果切分方案中包含

图 15-14 切分导致乘积变大
接下来思考哪个因子是最优的。在
如图 15-15 所示,当
贪心策略二:在切分方案中,最多只应存在两个
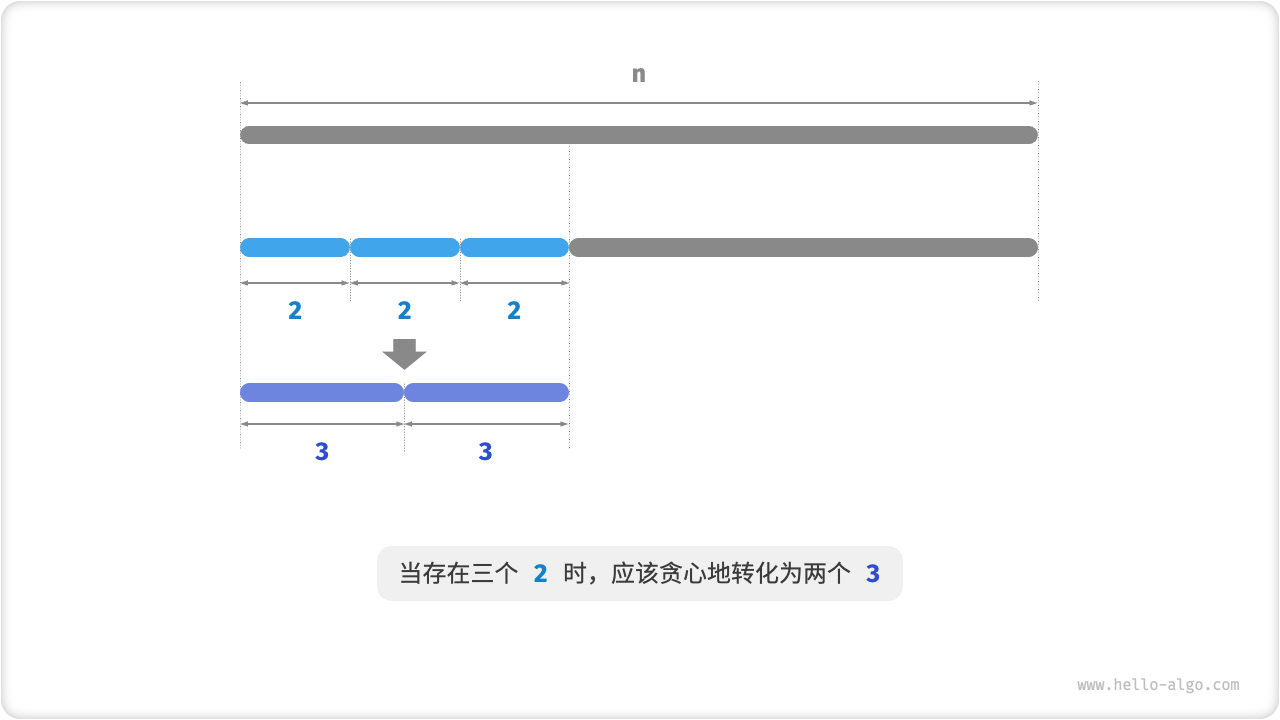
图 15-15 最优切分因子
总结以上,可推出以下贪心策略。
- 输入整数
- 当余数为
- 当余数为
- 当余数为
2. 代码实现
如图 15-16 所示,我们无须通过循环来切分整数,而可以利用向下整除运算得到
请注意,对于
max_product_cutting.cpp
/* 最大切分乘积:贪心 */
int maxProductCutting(int n) {
// 当 n <= 3 时,必须切分出一个 1
if (n <= 3) {
return 1 * (n - 1);
}
// 贪心地切分出 3 ,a 为 3 的个数,b 为余数
int a = n / 3;
int b = n % 3;
if (b == 1) {
// 当余数为 1 时,将一对 1 * 3 转化为 2 * 2
return (int)pow(3, a - 1) * 2 * 2;
}
if (b == 2) {
// 当余数为 2 时,不做处理
return (int)pow(3, a) * 2;
}
// 当余数为 0 时,不做处理
return (int)pow(3, a);
}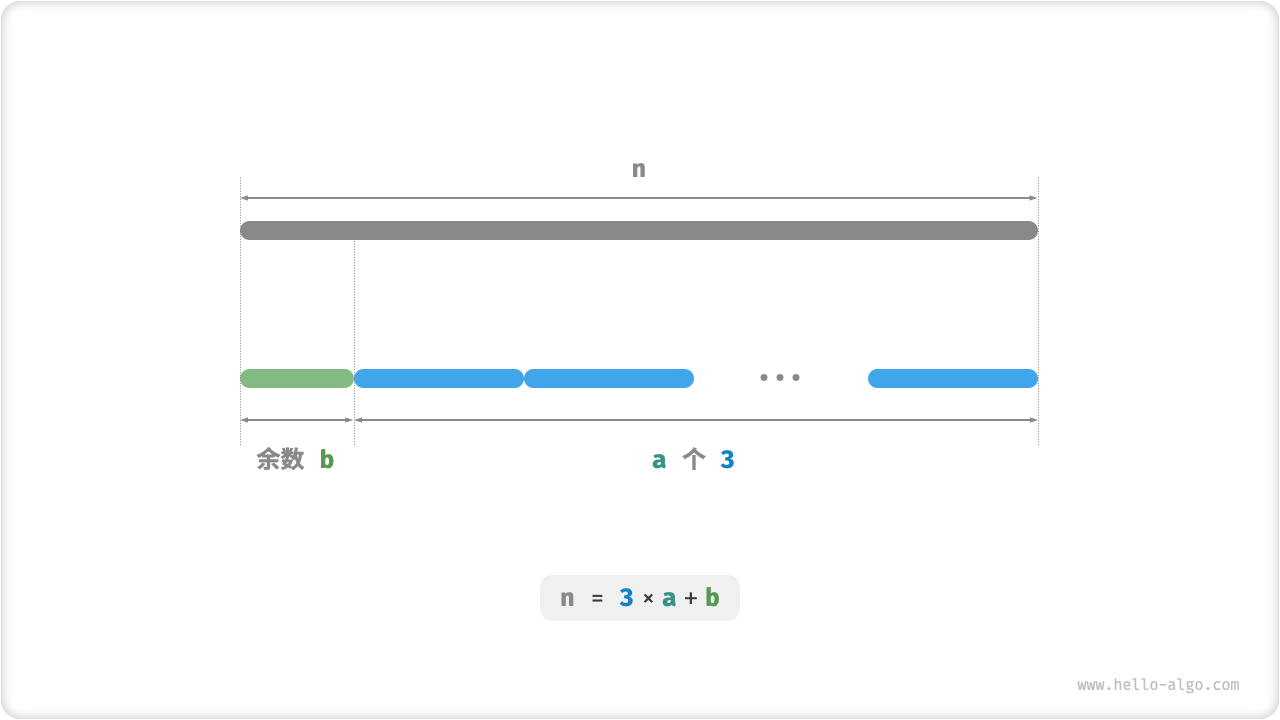
图 15-16 最大切分乘积的计算方法
时间复杂度取决于编程语言的幂运算的实现方法。以 Python 为例,常用的幂计算函数有三种。
- 运算符
**和函数pow()的时间复杂度均为 - 函数
math.pow()内部调用 C 语言库的pow()函数,其执行浮点取幂,时间复杂度为
变量
3. 正确性证明
使用反证法,只分析
- 所有因子
- 切分方案不包含
- 切分方案最多包含两个