图 15-3   分数背包问题的示例数据

分数背包和 0-1 背包整体上非常相似，状态包含当前物品 $i$ 和容量 $c$ ，目标是求不超过背包容量下的最大价值。

不同点在于，本题允许只选择物品的一部分。如图 15-4 所示，我们可以对物品任意地进行切分，并按照重量比例来计算物品价值。

1. 对于物品 $i$ ，它在单位重量下的价值为 $val[i-1]/wgt[i-1]$ ，简称为单位价值。
2. 假设放入一部分物品 $i$ ，重量为 $w$ ，则背包增加的价值为 $w\times val[i-1]/wgt[i-1]$ 。

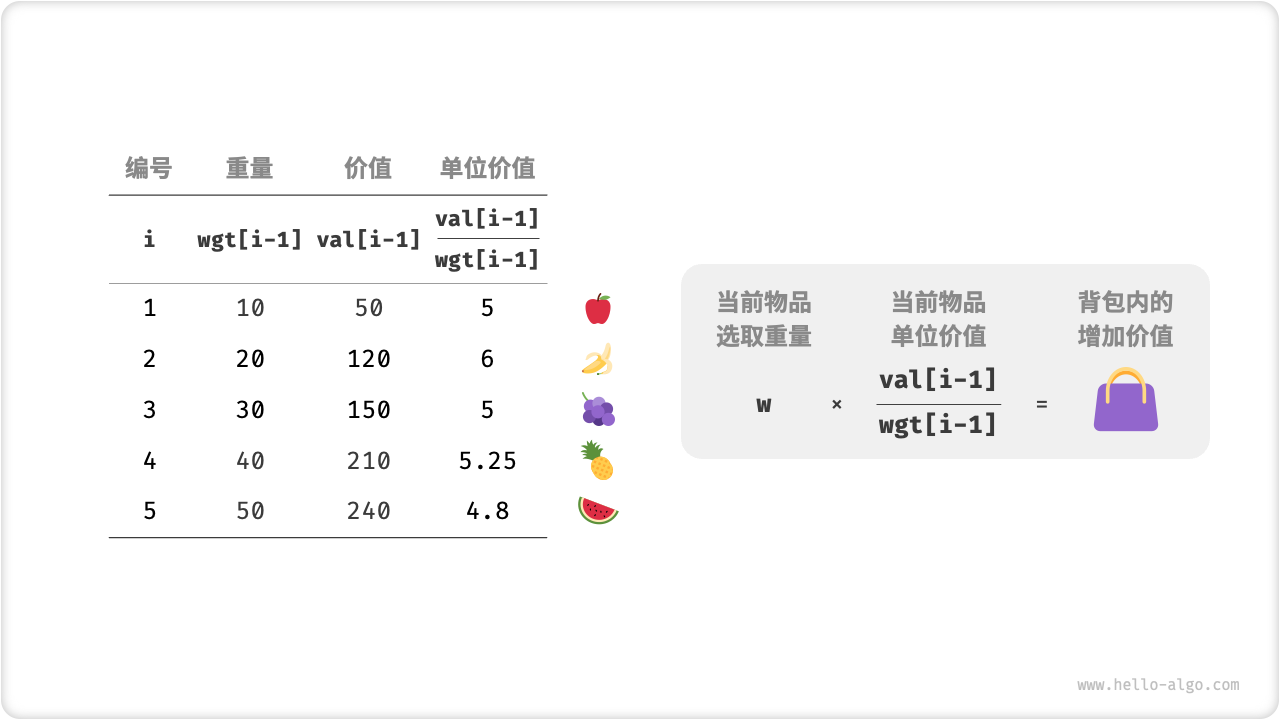
图 15-4   物品在单位重量下的价值

1.   贪心策略确定

最大化背包内物品总价值，本质上是要最大化单位重量下的物品价值。由此便可推出图 15-5 所示的贪心策略。

1. 将物品按照单位价值从高到低进行排序。
2. 遍历所有物品，每轮贪心地选择单位价值最高的物品。
3. 若剩余背包容量不足，则使用当前物品的一部分填满背包即可。

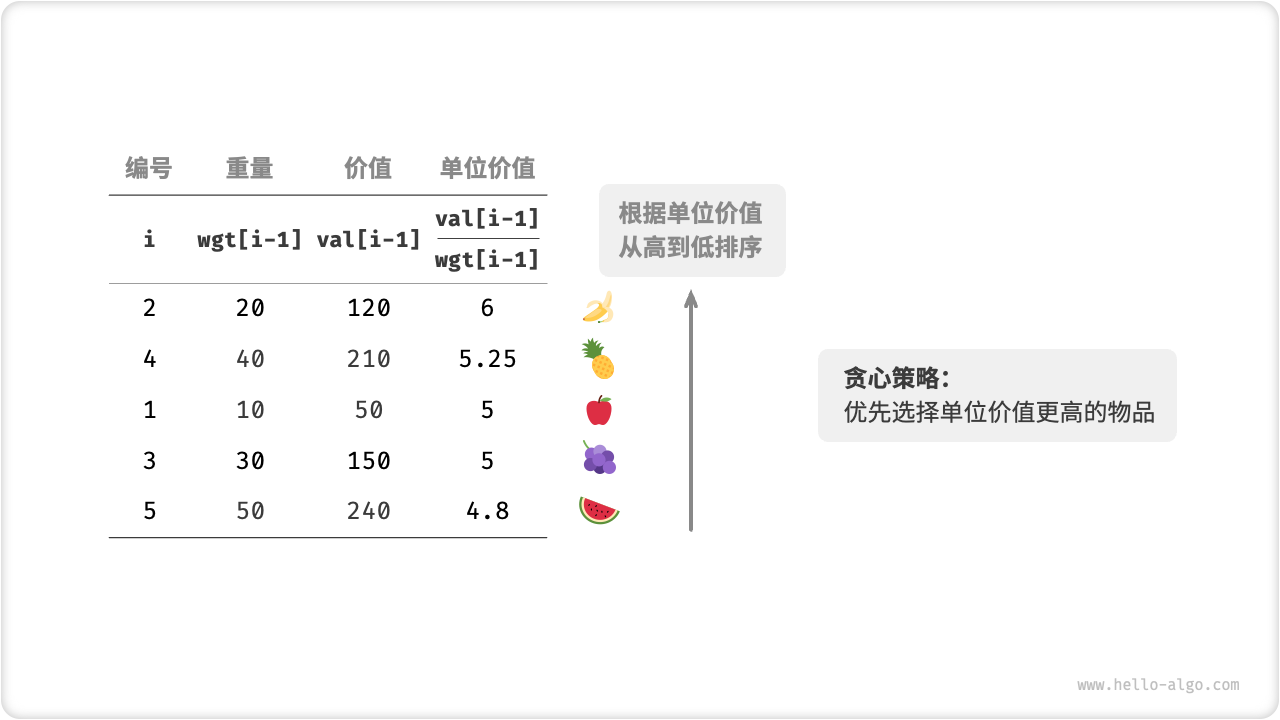
图 15-5   分数背包的贪心策略

2.   代码实现

我们建立了一个物品类 Item ，以便将物品按照单位价值进行排序。循环进行贪心选择，当背包已满时跳出并返回解。

fractional_knapsack.cpp

/* 物品 */
class Item {
  public:
    int w; // 物品重量
    int v; // 物品价值

    Item(int w, int v) : w(w), v(v) {
    }
};

/* 分数背包：贪心 */
double fractionalKnapsack(vector<int> &wgt, vector<int> &val, int cap) {
    // 创建物品列表，包含两个属性：重量、价值
    vector<Item> items;
    for (int i = 0; i < wgt.size(); i++) {
        items.push_back(Item(wgt[i], val[i]));
    }
    // 按照单位价值 item.v / item.w 从高到低进行排序
    sort(items.begin(), items.end(), [](Item &a, Item &b) { return (double)a.v / a.w > (double)b.v / b.w; });
    // 循环贪心选择
    double res = 0;
    for (auto &item : items) {
        if (item.w <= cap) {
            // 若剩余容量充足，则将当前物品整个装进背包
            res += item.v;
            cap -= item.w;
        } else {
            // 若剩余容量不足，则将当前物品的一部分装进背包
            res += (double)item.v / item.w * cap;
            // 已无剩余容量，因此跳出循环
            break;
        }
    }
    return res;
}

最差情况下，需要遍历整个物品列表，因此时间复杂度为 $O(n)$ ，其中 $n$ 为物品数量。

由于初始化了一个 Item 对象列表，因此空间复杂度为 $O(n)$ 。

3.   正确性证明

采用反证法。假设物品 $x$ 是单位价值最高的物品，使用某算法求得最大价值为 res ，但该解中不包含物品 $x$ 。

现在从背包中拿出单位重量的任意物品，并替换为单位重量的物品 $x$ 。由于物品 $x$ 的单位价值最高，因此替换后的总价值一定大于 res 。这与 res 是最优解矛盾，说明最优解中必须包含物品 $x$ 。

对于该解中的其他物品，我们也可以构建出上述矛盾。总而言之，单位价值更大的物品总是更优选择，这说明贪心策略是有效的。

如图 15-6 所示，如果将物品重量和物品单位价值分别看作一个 2D 图表的横轴和纵轴，则分数背包问题可被转化为“求在有限横轴区间下的最大围成面积”。这个类比可以帮助我们从几何角度理解贪心策略的有效性。

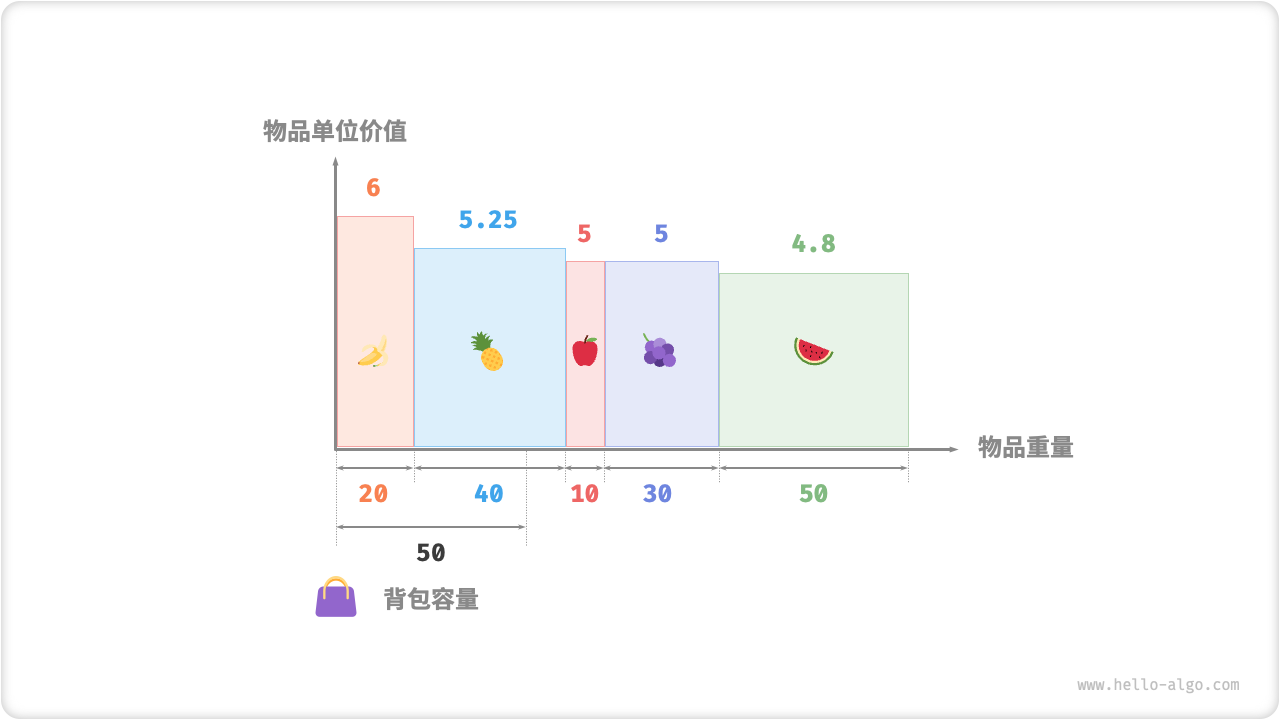
图 15-6   分数背包问题的几何表示