
C++归并排序
「归并排序 merge sort」是一种基于分治策略的排序算法,包含图 11-10 所示的“划分”和“合并”阶段。
- 划分阶段:通过递归不断地将数组从中点处分开,将长数组的排序问题转换为短数组的排序问题。
- 合并阶段:当子数组长度为 1 时终止划分,开始合并,持续地将左右两个较短的有序数组合并为一个较长的有序数组,直至结束。
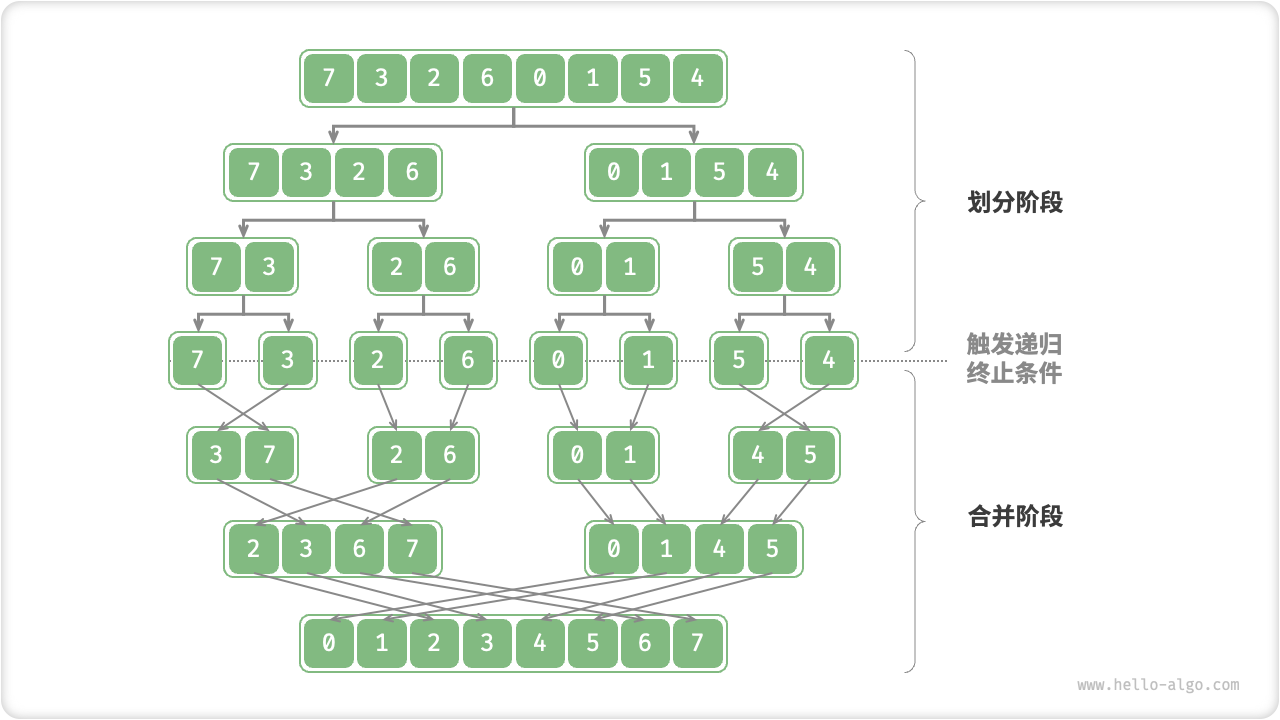
图 11-10 归并排序的划分与合并阶段
11.6.1 算法流程
如图 11-11 所示,“划分阶段”从顶至底递归地将数组从中点切分为两个子数组。
- 计算数组中点
mid ,递归划分左子数组(区间 [left, mid] )和右子数组(区间 [mid + 1, right] )。 - 递归执行步骤 1. ,直至子数组区间长度为 1 时,终止递归划分。
“合并阶段”从底至顶地将左子数组和右子数组合并为一个有序数组。需要注意的是,从长度为 1 的子数组开始合并,合并阶段中的每个子数组都是有序的。
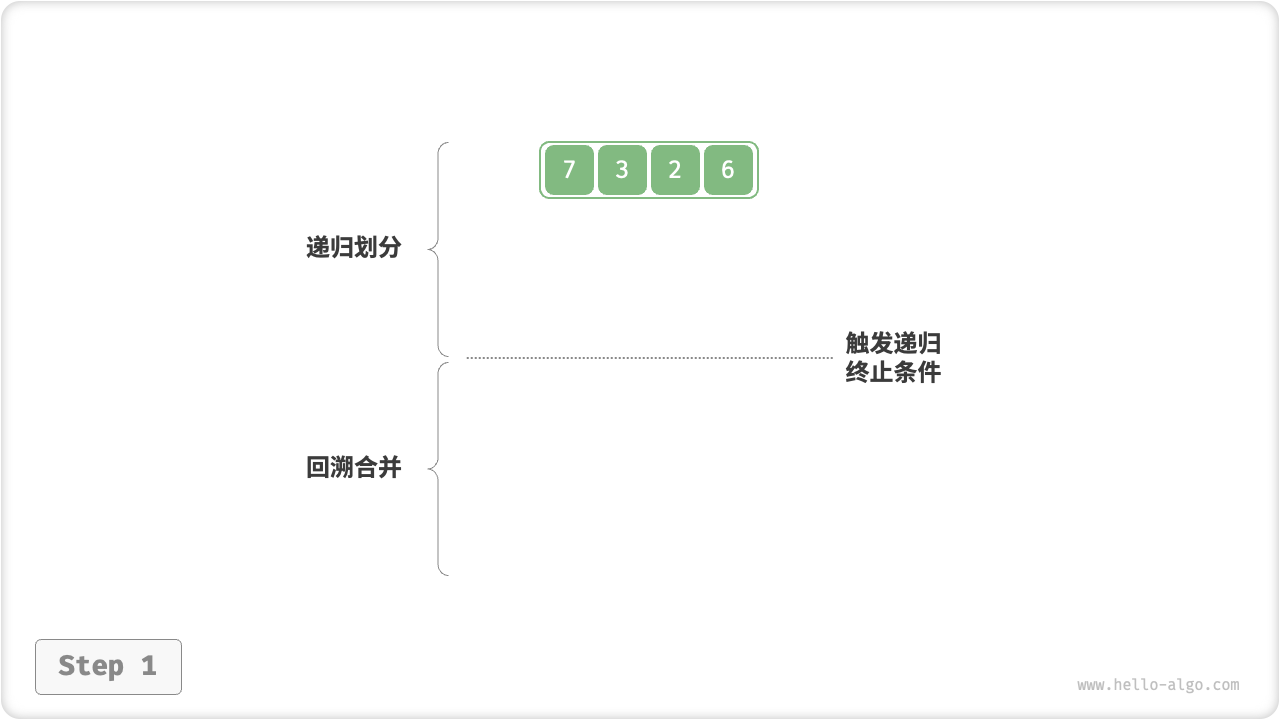
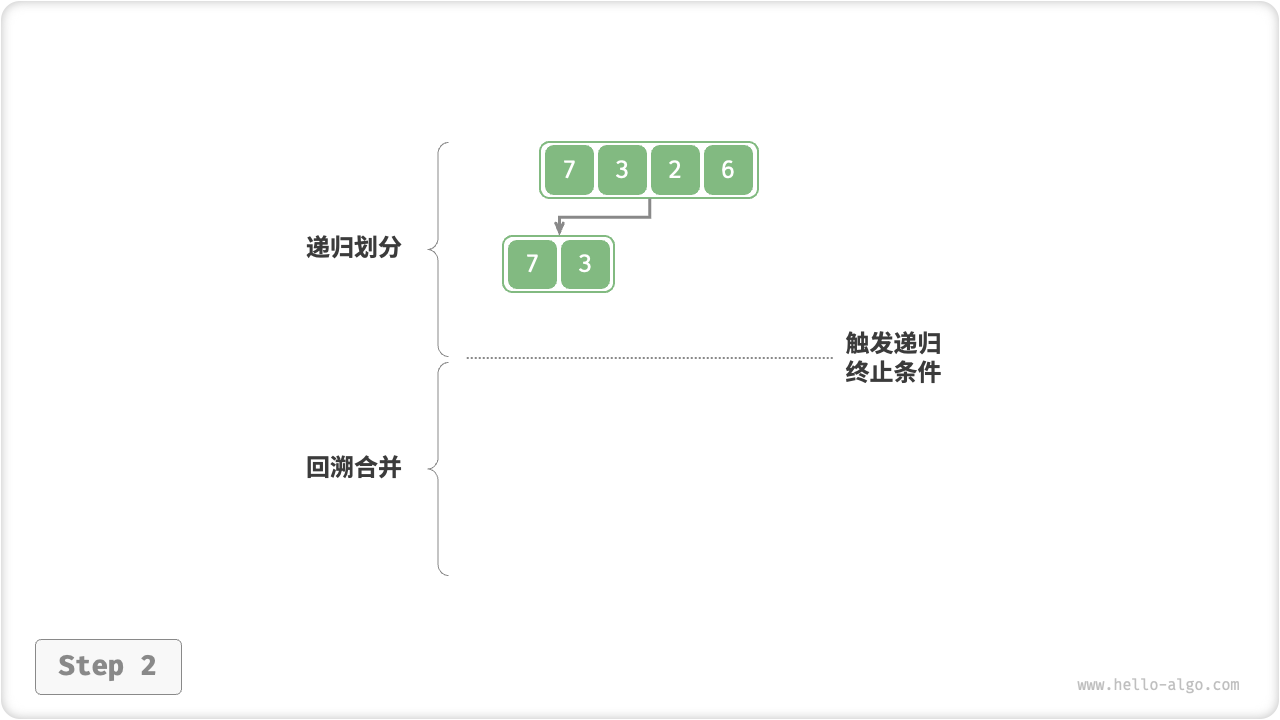
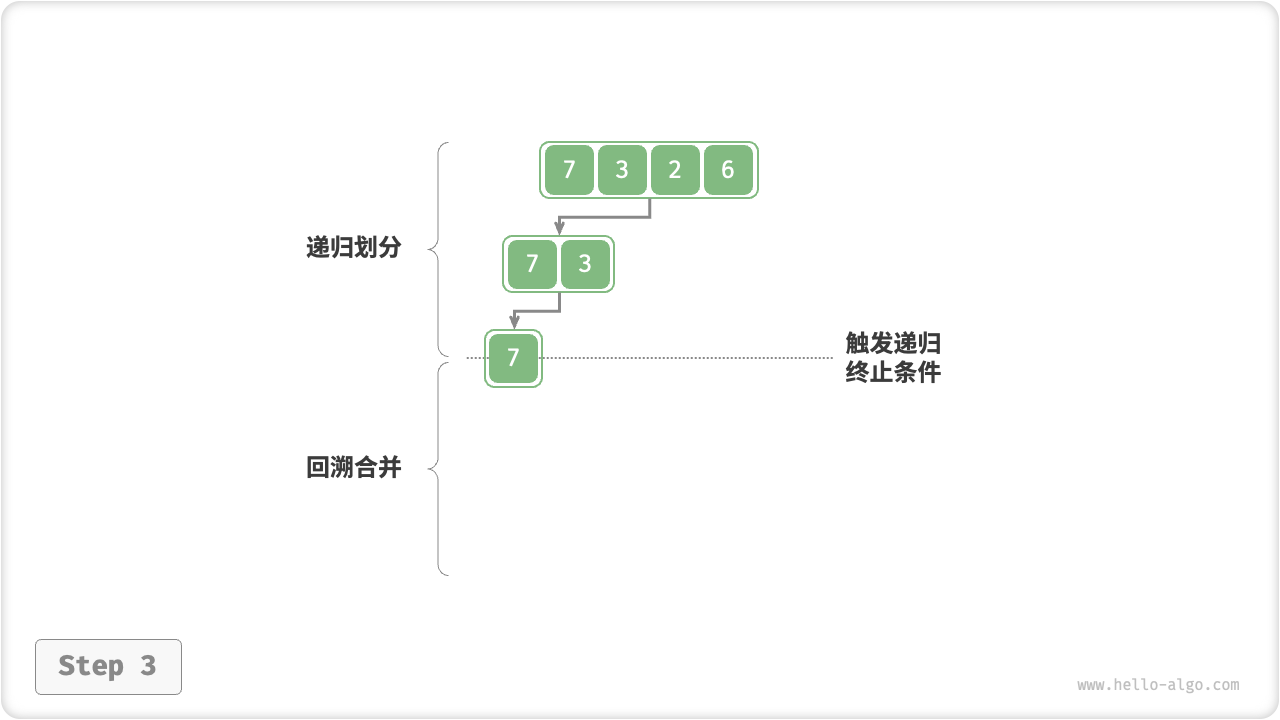
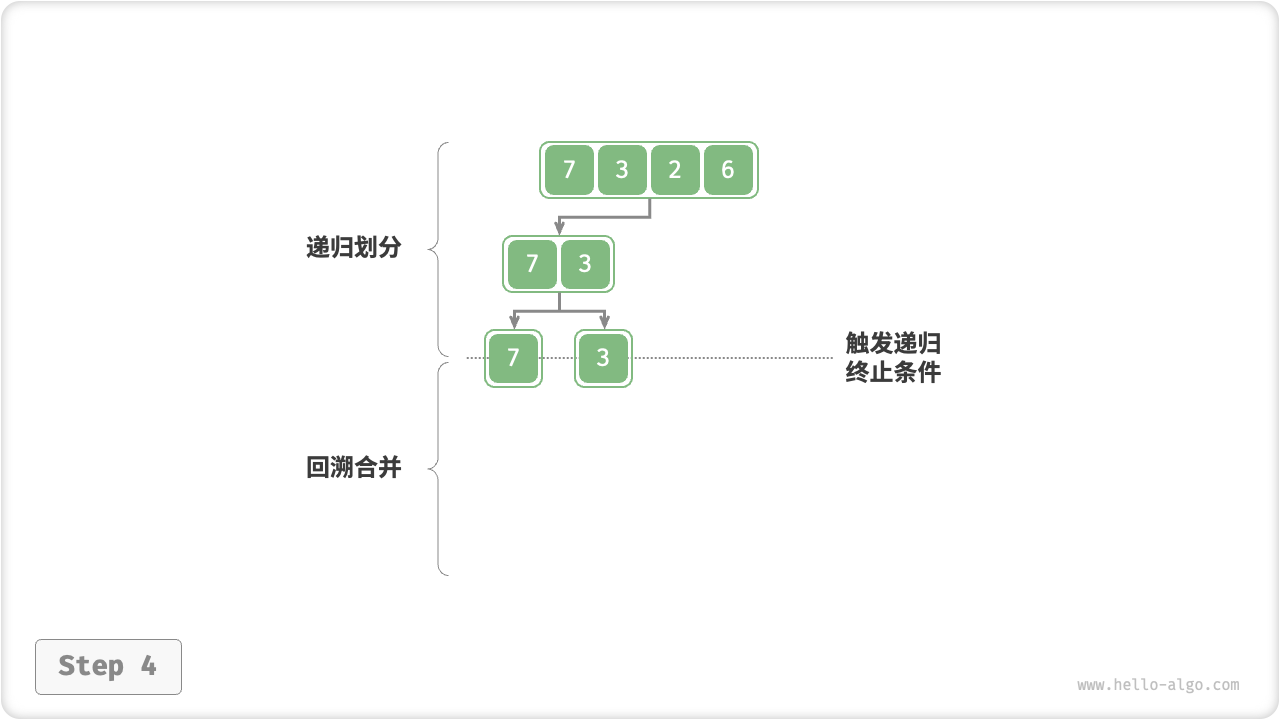
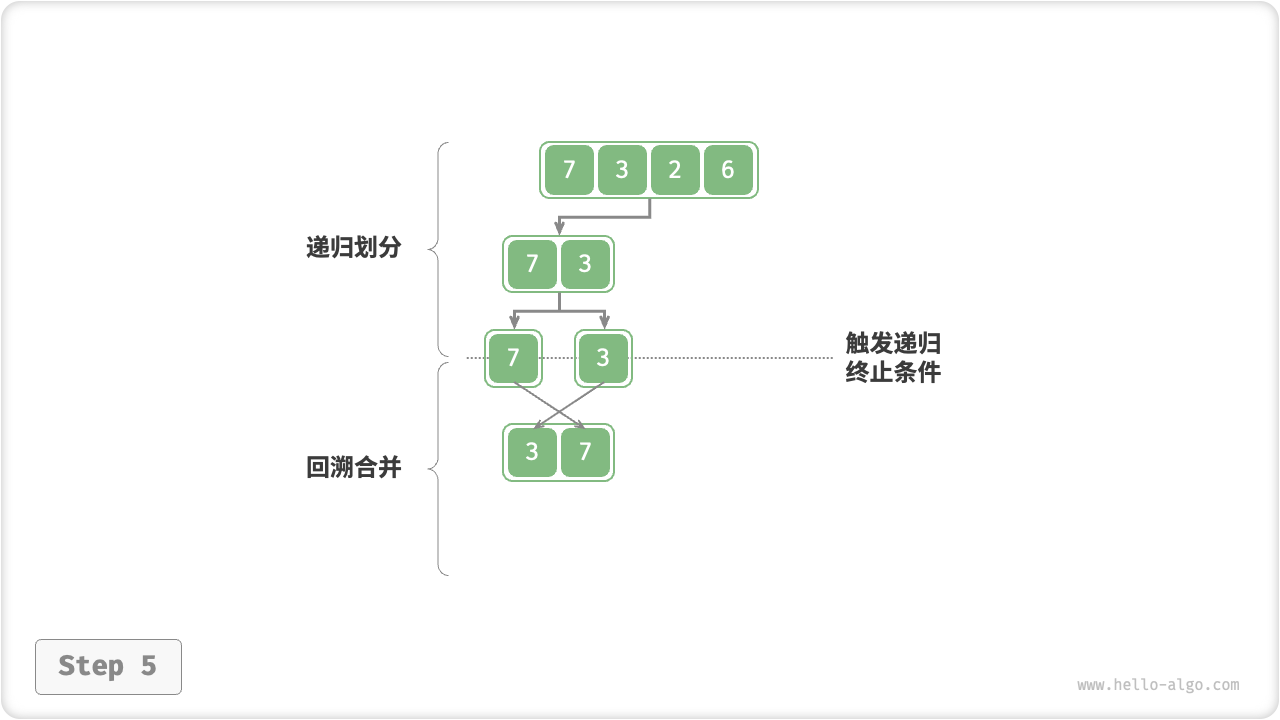
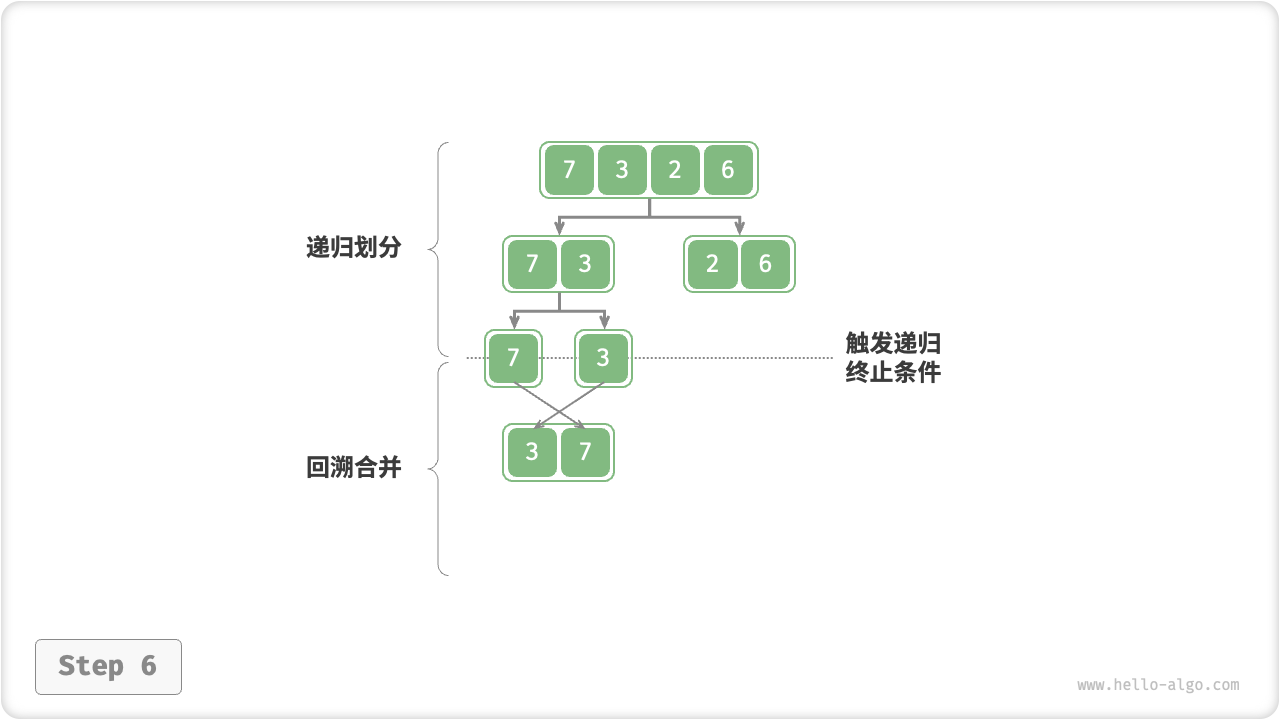
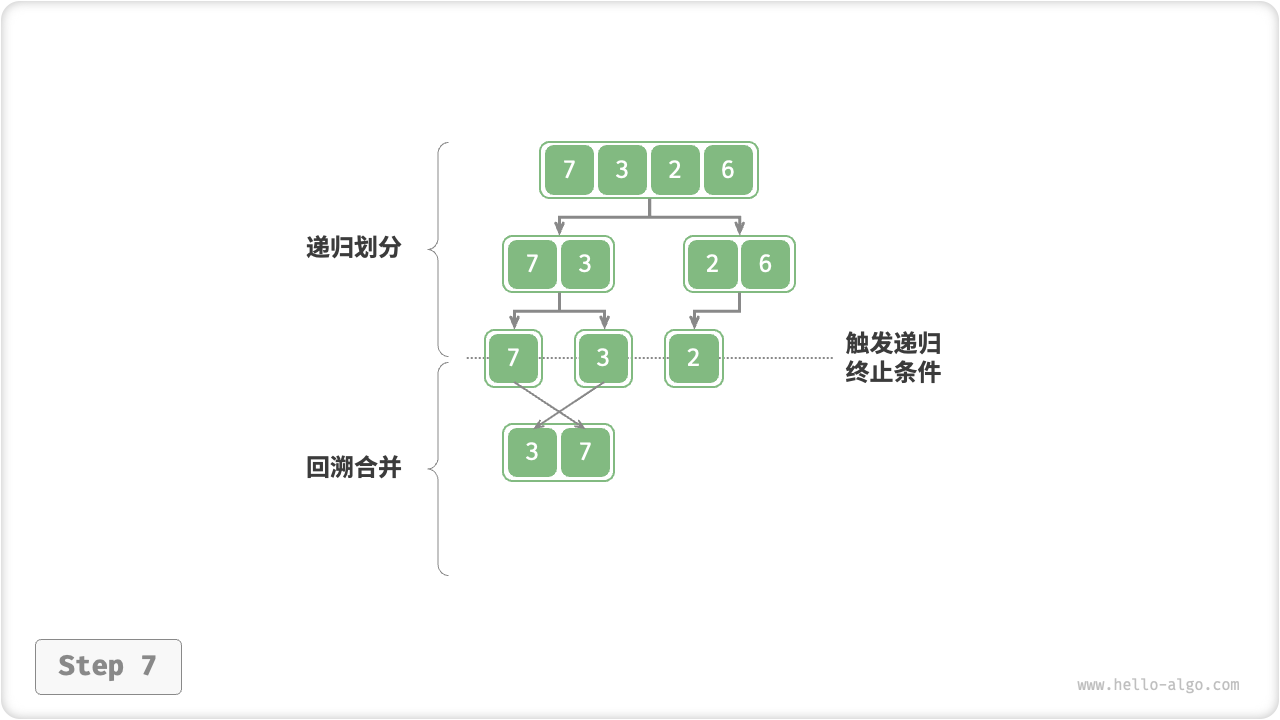

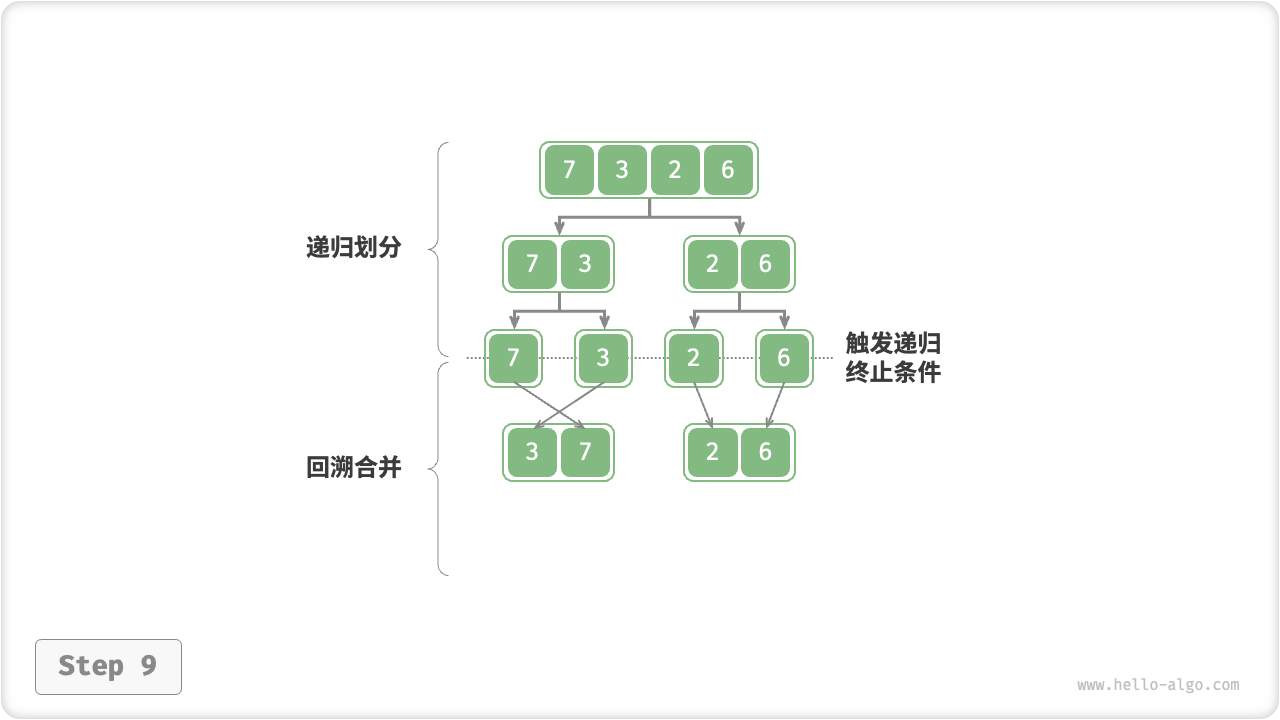
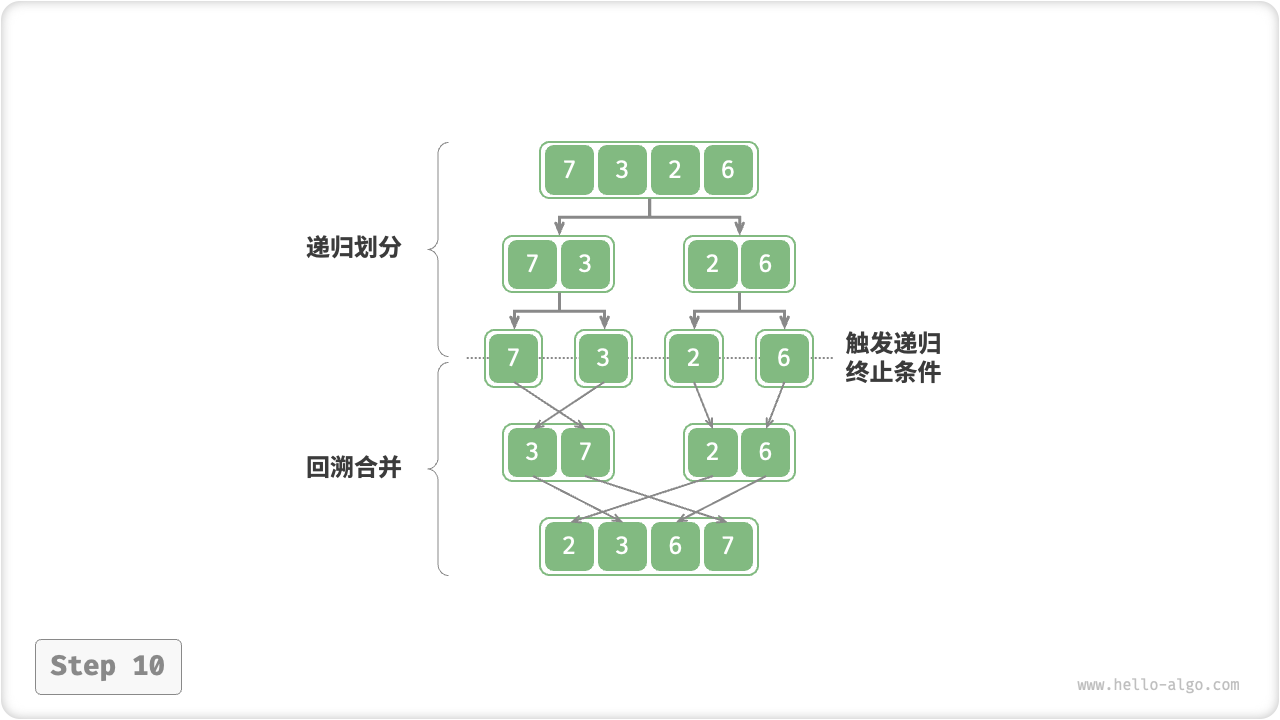
图 11-11 归并排序步骤
观察发现,归并排序与二叉树后序遍历的递归顺序是一致的。
- 后序遍历:先递归左子树,再递归右子树,最后处理根节点。
- 归并排序:先递归左子数组,再递归右子数组,最后处理合并。
merge_sort.cpp
/* 合并左子数组和右子数组 */
// 左子数组区间 [left, mid]
// 右子数组区间 [mid + 1, right]
void merge(vector<int> &nums, int left, int mid, int right) {
// 初始化辅助数组
vector<int> tmp(nums.begin() + left, nums.begin() + right + 1);
// 左子数组的起始索引和结束索引
int leftStart = left - left, leftEnd = mid - left;
// 右子数组的起始索引和结束索引
int rightStart = mid + 1 - left, rightEnd = right - left;
// i, j 分别指向左子数组、右子数组的首元素
int i = leftStart, j = rightStart;
// 通过覆盖原数组 nums 来合并左子数组和右子数组
for (int k = left; k <= right; k++) {
// 若“左子数组已全部合并完”,则选取右子数组元素,并且 j++
if (i > leftEnd)
nums[k] = tmp[j++];
// 否则,若“右子数组已全部合并完”或“左子数组元素 <= 右子数组元素”,则选取左子数组元素,并且 i++
else if (j > rightEnd || tmp[i] <= tmp[j])
nums[k] = tmp[i++];
// 否则,若“左右子数组都未全部合并完”且“左子数组元素 > 右子数组元素”,则选取右子数组元素,并且 j++
else
nums[k] = tmp[j++];
}
}
/* 归并排序 */
void mergeSort(vector<int> &nums, int left, int right) {
// 终止条件
if (left >= right)
return; // 当子数组长度为 1 时终止递归
// 划分阶段
int mid = (left + right) / 2; // 计算中点
mergeSort(nums, left, mid); // 递归左子数组
mergeSort(nums, mid + 1, right); // 递归右子数组
// 合并阶段
merge(nums, left, mid, right);
}实现合并函数 merge() 存在以下难点。
- 需要特别注意各个变量的含义。nums 的待合并区间为 [left, right] ,但由于 tmp 仅复制了 nums 该区间的元素,因此 tmp 对应区间为 [0, right - left] 。
- 在比较 tmp[i] 和 tmp[j] 的大小时,还需考虑子数组遍历完成后的索引越界问题,即 i > leftEnd 和 j > rightEnd 的情况。索引越界的优先级是最高的,如果左子数组已经被合并完了,那么不需要继续比较,直接合并右子数组元素即可。
算法特性
- 时间复杂度 O(nlogn)、非自适应排序:划分产生高度为 logn 的递归树,每层合并的总操作数量为 n ,因此总体时间复杂度为 O(nlogn) 。
- 空间复杂度 O(n)、非原地排序:递归深度为 logn ,使用 O(logn) 大小的栈帧空间。合并操作需要借助辅助数组实现,使用 O(n) 大小的额外空间。
- 稳定排序:在合并过程中,相等元素的次序保持不变。
链表排序 *
对于链表,归并排序相较于其他排序算法具有显著优势,可以将链表排序任务的空间复杂度优化至 O(1) 。
- 划分阶段:可以通过使用“迭代”替代“递归”来实现链表划分工作,从而省去递归使用的栈帧空间。
- 合并阶段:在链表中,节点增删操作仅需改变引用(指针)即可实现,因此合并阶段(将两个短有序链表合并为一个长有序链表)无须创建额外链表。
具体实现细节比较复杂,有兴趣的同学可以查阅相关资料进行学习。