前述的几种排序算法都属于“基于比较的排序算法”，它们通过比较元素间的大小来实现排序。此类排序算法的时间复杂度无法超越 O(nlog⁡n) 。接下来，我们将探讨几种“非比较排序算法”，它们的时间复杂度可以达到线性阶。

「桶排序 bucket sort」是分治策略的一个典型应用。它通过设置一些具有大小顺序的桶，每个桶对应一个数据范围，将数据平均分配到各个桶中；然后，在每个桶内部分别执行排序；最终按照桶的顺序将所有数据合并。

11.8.1   算法流程¶

考虑一个长度为 n 的数组，元素是范围 [0,1) 的浮点数。桶排序的流程如图 11-13 所示。

1. 初始化 k 个桶，将 n 个元素分配到 k 个桶中。
2. 对每个桶分别执行排序（本文采用编程语言的内置排序函数）。
3. 按照桶的从小到大的顺序，合并结果。

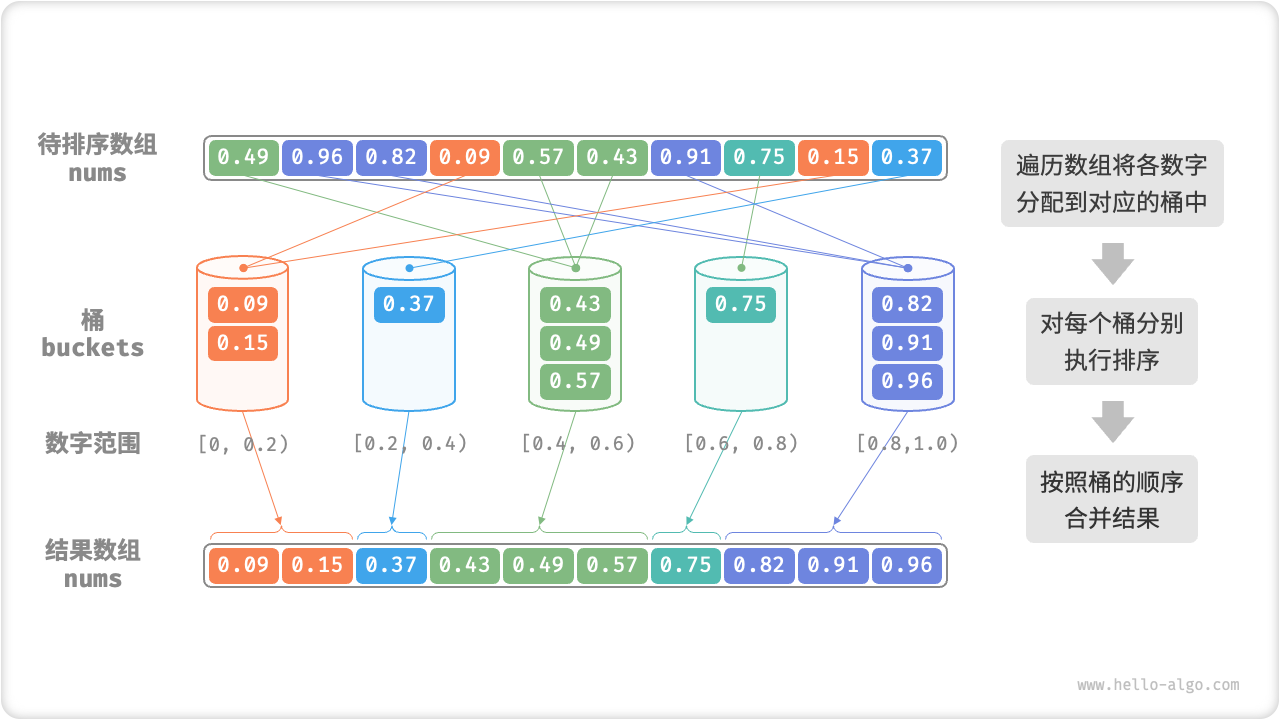
图 11-13   桶排序算法流程

bucket_sort.cpp

/* 桶排序 */
void bucketSort(vector<float> &nums) {
    // 初始化 k = n/2 个桶，预期向每个桶分配 2 个元素
    int k = nums.size() / 2;
    vector<vector<float>> buckets(k);
    // 1. 将数组元素分配到各个桶中
    for (float num : nums) {
        // 输入数据范围 [0, 1)，使用 num * k 映射到索引范围 [0, k-1]
        int i = num * k;
        // 将 num 添加进桶 bucket_idx
        buckets[i].push_back(num);
    }
    // 2. 对各个桶执行排序
    for (vector<float> &bucket : buckets) {
        // 使用内置排序函数，也可以替换成其他排序算法
        sort(bucket.begin(), bucket.end());
    }
    // 3. 遍历桶合并结果
    int i = 0;
    for (vector<float> &bucket : buckets) {
        for (float num : bucket) {
            nums[i++] = num;
        }
    }
}

11.8.2   算法特性

• 时间复杂度 $O(n+k)$ ：假设元素在各个桶内平均分布，那么每个桶内的元素数量为 $\frac{n}{k}$ 。假设排序单个桶使用 $O(\frac{n}{k}\log \frac{n}{k})$ 时间，则排序所有桶使用 $O(n\log \frac{n}{k})$ 时间。当桶数量 $k$ 比较大时，时间复杂度则趋向于 $O(n)$ 。合并结果时需要遍历所有桶和元素，花费 $O(n+k)$ 时间。
• 自适应排序：在最坏情况下，所有数据被分配到一个桶中，且排序该桶使用 $O(n^2)$ 时间。
• 空间复杂度 $O(n+k)$、非原地排序：需要借助 $k$ 个桶和总共 $n$ 个元素的额外空间。
• 桶排序是否稳定取决于排序桶内元素的算法是否稳定。

11.8.3   如何实现平均分配

桶排序的时间复杂度理论上可以达到 O(n) ，关键在于将元素均匀分配到各个桶中，因为实际数据往往不是均匀分布的。例如，我们想要将淘宝上的所有商品按价格范围平均分配到 10 个桶中，但商品价格分布不均，低于 100 元的非常多，高于 1000 元的非常少。若将价格区间平均划分为 10 份，各个桶中的商品数量差距会非常大。

为实现平均分配，我们可以先设定一个大致的分界线，将数据粗略地分到 3 个桶中。分配完毕后，再将商品较多的桶继续划分为 3 个桶，直至所有桶中的元素数量大致相等。

如图 11-14 所示，这种方法本质上是创建一个递归树，目标是让叶节点的值尽可能平均。当然，不一定要每轮将数据划分为 3 个桶，具体划分方式可根据数据特点灵活选择。

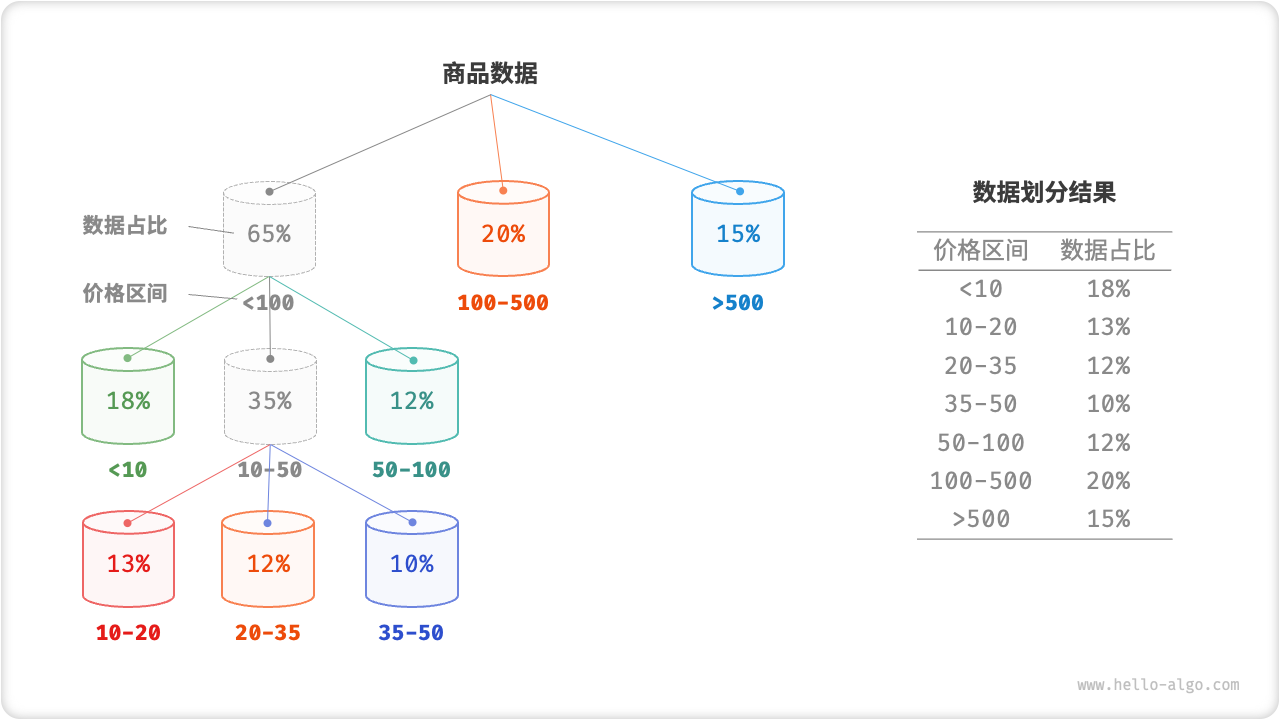
图 11-14   递归划分桶

如果我们提前知道商品价格的概率分布，则可以根据数据概率分布设置每个桶的价格分界线。值得注意的是，数据分布并不一定需要特意统计，也可以根据数据特点采用某种概率模型进行近似。

如图 11-15 所示，我们假设商品价格服从正态分布，这样就可以合理地设定价格区间，从而将商品平均分配到各个桶中。

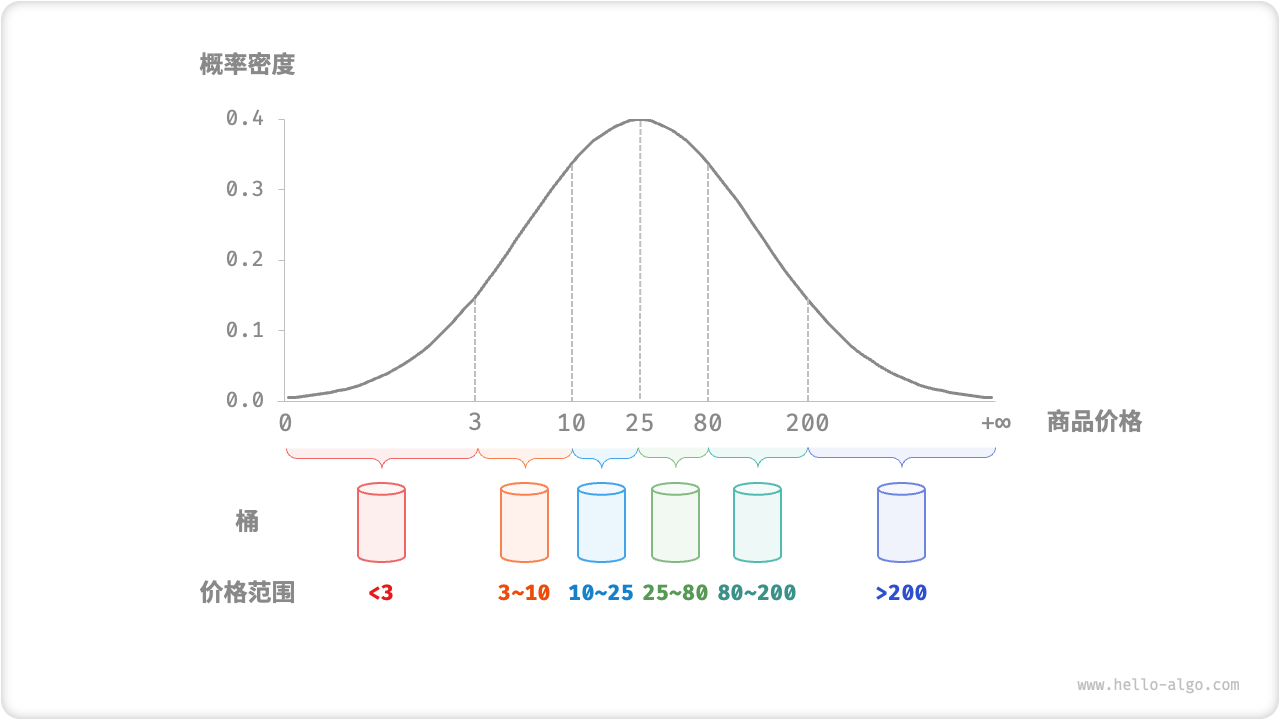
图 11-15   根据概率分布划分桶