在上节中，我们学习了动态规划是如何通过子问题分解来求解问题的。实际上，子问题分解是一种通用的算法思路，在分治、动态规划、回溯中的侧重点不同。

• 分治算法递归地将原问题划分为多个相互独立的子问题，直至最小子问题，并在回溯中合并子问题的解，最终得到原问题的解。
• 动态规划也对问题进行递归分解，但与分治算法的主要区别是，动态规划中的子问题是相互依赖的，在分解过程中会出现许多重叠子问题。
• 回溯算法在尝试和回退中穷举所有可能的解，并通过剪枝避免不必要的搜索分支。原问题的解由一系列决策步骤构成，我们可以将每个决策步骤之前的子序列看作为一个子问题。

实际上，动态规划常用来求解最优化问题，它们不仅包含重叠子问题，还具有另外两大特性：最优子结构、无后效性。

最优子结构

我们对爬楼梯问题稍作改动，使之更加适合展示最优子结构概念。

如图 14-6 所示，若第 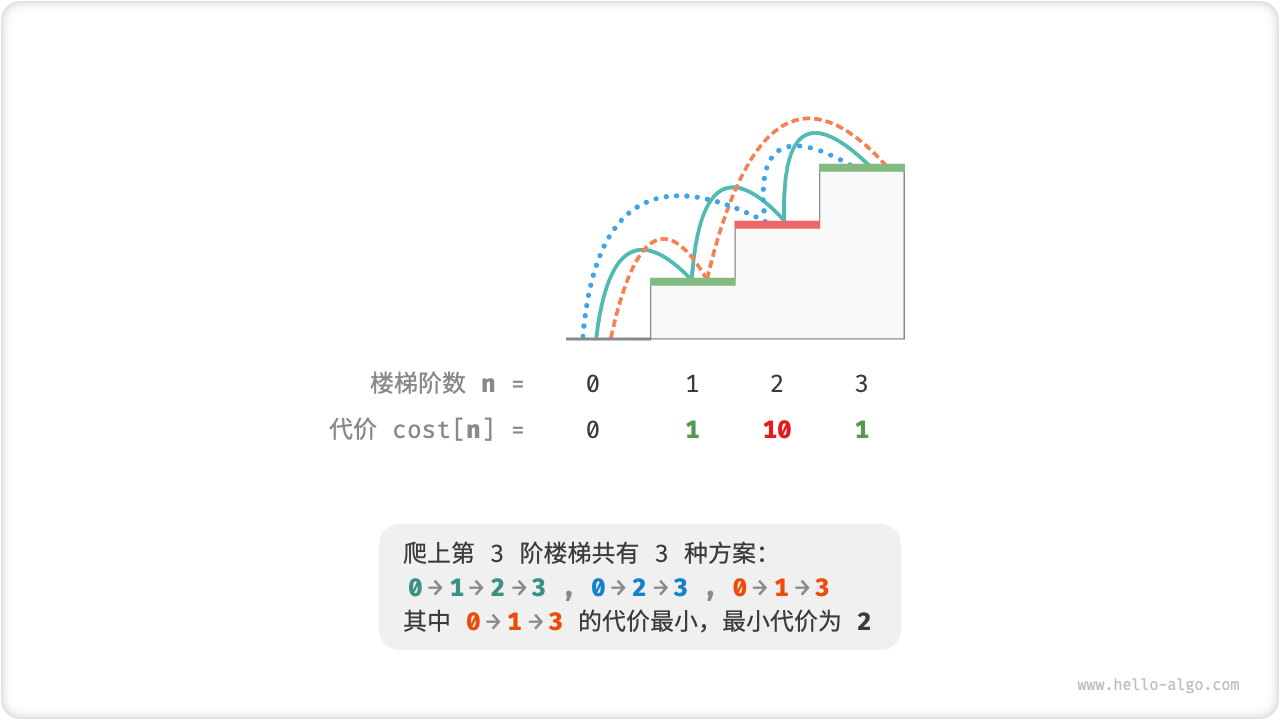$1$、$2$、$3$ 阶的代价分别为 $1$、$10$、$1$ ，则从地面爬到第 $3$ 阶的最小代价为 $2$ 。

图 14-6   爬到第 3 阶的最小代价

设 $dp[i]$ 为爬到第 $i$ 阶累计付出的代价，由于第 $i$ 阶只可能从 $i-1$ 阶或 $i-2$ 阶走来，因此 $dp[i]$ 只可能等于 $dp[i-1]+cost[i]$ 或 $dp[i-2]+cost[i]$ 。为了尽可能减少代价，我们应该选择两者中较小的那一个：

这便可以引出最优子结构的含义：原问题的最优解是从子问题的最优解构建得来的。

本题显然具有最优子结构：我们从两个子问题最优解 $dp[i-1]$ 和 $dp[i-2]$ 中挑选出较优的那一个，并用它构建出原问题 $dp[i]$ 的最优解。

那么，上节的爬楼梯题目有没有最优子结构呢？它的目标是求解方案数量，看似是一个计数问题，但如果换一种问法：“求解最大方案数量”。我们意外地发现，虽然题目修改前后是等价的，但最优子结构浮现出来了：第 $n$ 阶最大方案数量等于第 $n-1$ 阶和第 $n-2$ 阶最大方案数量之和。所以说，最优子结构的解释方式比较灵活，在不同问题中会有不同的含义。

根据状态转移方程，以及初始状态 $dp[1]=cost[1]$ 和 $dp[2]=cost[2]$ ，我们就可以得到动态规划代码。

min_cost_climbing_stairs_dp.cpp

/* 爬楼梯最小代价：动态规划 */
int minCostClimbingStairsDP(vector<int> &cost) {
    int n = cost.size() - 1;
    if (n == 1 || n == 2)
        return cost[n];
    // 初始化 dp 表，用于存储子问题的解
    vector<int> dp(n + 1);
    // 初始状态：预设最小子问题的解
    dp[1] = cost[1];
    dp[2] = cost[2];
    // 状态转移：从较小子问题逐步求解较大子问题
    for (int i = 3; i <= n; i++) {
        dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
    }
    return dp[n];
}

图 14-7 展示了以上代码的动态规划过程。

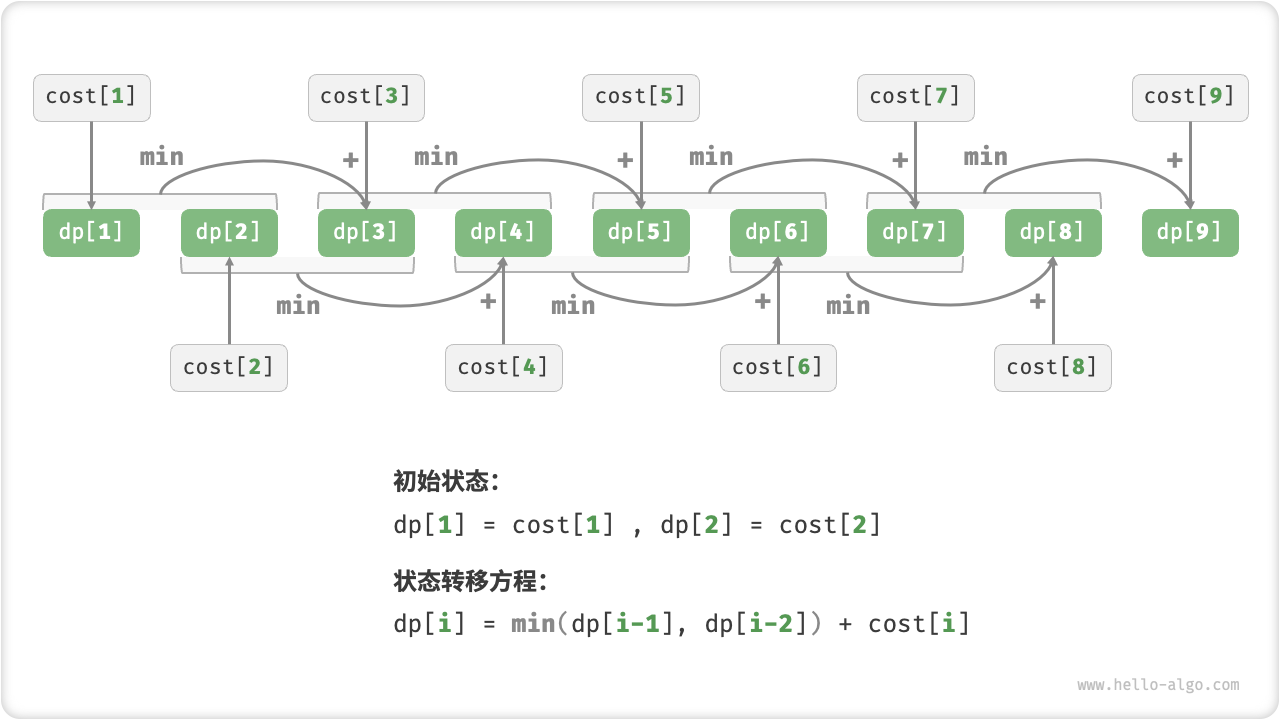
图 14-7   爬楼梯最小代价的动态规划过程

本题也可以进行空间优化，将一维压缩至零维，使得空间复杂度从 $O(n)$ 降低至 $O(1)$ 。

min_cost_climbing_stairs_dp.cpp

/* 爬楼梯最小代价：空间优化后的动态规划 */
int minCostClimbingStairsDPComp(vector<int> &cost) {
    int n = cost.size() - 1;
    if (n == 1 || n == 2)
        return cost[n];
    int a = cost[1], b = cost[2];
    for (int i = 3; i <= n; i++) {
        int tmp = b;
        b = min(a, tmp) + cost[i];
        a = tmp;
    }
    return b;
}

无后效性¶

无后效性是动态规划能够有效解决问题的重要特性之一，定义为：给定一个确定的状态，它的未来发展只与当前状态有关，而与当前状态过去所经历过的所有状态无关。

以爬楼梯问题为例，给定状态 $i$ ，它会发展出状态 $i+1$ 和状态 $i+2$ ，分别对应跳 $1$ 步和跳 $2$ 步。在做出这两种选择时，我们无须考虑状态 $i$ 之前的状态，它们对状态 $i$ 的未来没有影响。

然而，如果我们向爬楼梯问题添加一个约束，情况就不一样了。

例如图 14-8 ，爬上第 $3$ 阶仅剩 $2$ 种可行方案，其中连续三次跳 $1$ 阶的方案不满足约束条件，因此被舍弃。

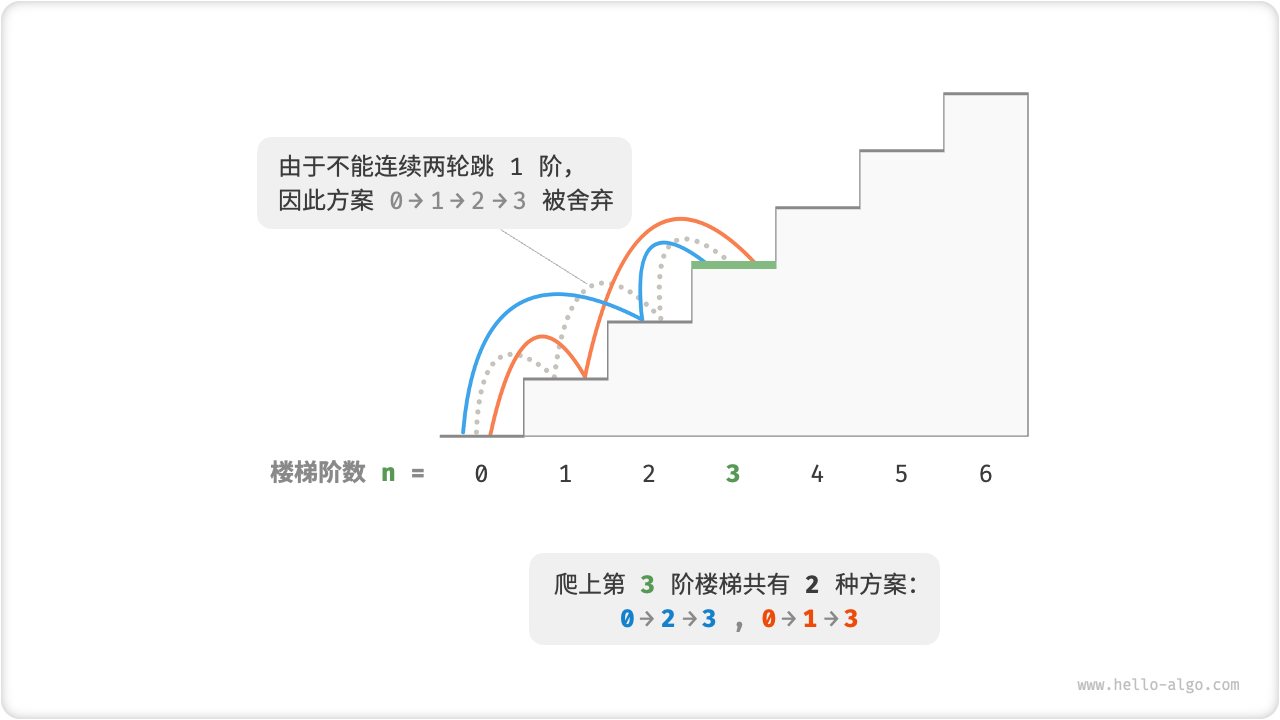
图 14-8   带约束爬到第 3 阶的方案数量

在该问题中，如果上一轮是跳 $1$ 阶上来的，那么下一轮就必须跳 $2$ 阶。这意味着，下一步选择不能由当前状态（当前楼梯阶数）独立决定，还和前一个状态（上轮楼梯阶数）有关。

不难发现，此问题已不满足无后效性，状态转移方程 $dp[i]=dp[i-1]+dp[i-2]$ 也失效了，因为 $dp[i-1]$ 代表本轮跳 $1$ 阶，但其中包含了许多“上一轮跳 $1$ 阶上来的”方案，而为了满足约束，我们就不能将 $dp[i-1]$ 直接计入 $dp[i]$ 中。

为此，我们需要扩展状态定义：状态 $[i,j]$ 表示处在第 $i$ 阶、并且上一轮跳了 $j$ 阶，其中 $j\in \{1,2\}$ 。此状态定义有效地区分了上一轮跳了 $1$ 阶还是 $2$ 阶，我们可以据此来决定下一步该怎么跳。

• 当 $j$ 等于 $1$ ，即上一轮跳了 $1$ 阶时，这一轮只能选择跳 $2$ 阶。
• 当 $j$ 等于 $2$ ，即上一轮跳了 $2$ 阶时，这一轮可选择跳 $1$ 阶或跳 $2$ 阶。

如图 14-9 所示，在该定义下，$dp[i,j]$ 表示状态 $[i,j]$ 对应的方案数。此时状态转移方程为：

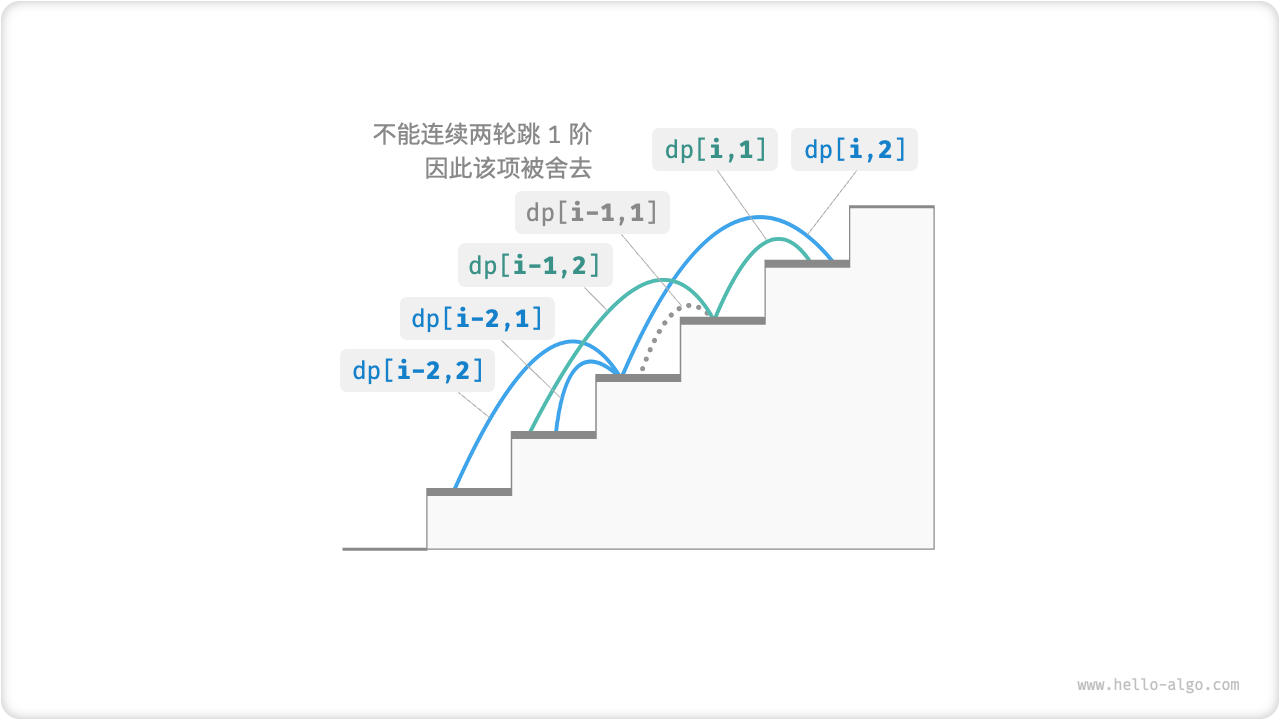
图 14-9   考虑约束下的递推关系

最终，返回 $dp[n,1]+dp[n,2]$ 即可，两者之和代表爬到第 $n$ 阶的方案总数。

climbing_stairs_constraint_dp.cpp

/* 带约束爬楼梯：动态规划 */
int climbingStairsConstraintDP(int n) {
    if (n == 1 || n == 2) {
        return 1;
    }
    // 初始化 dp 表，用于存储子问题的解
    vector<vector<int>> dp(n + 1, vector<int>(3, 0));
    // 初始状态：预设最小子问题的解
    dp[1][1] = 1;
    dp[1][2] = 0;
    dp[2][1] = 0;
    dp[2][2] = 1;
    // 状态转移：从较小子问题逐步求解较大子问题
    for (int i = 3; i <= n; i++) {
        dp[i][1] = dp[i - 1][2];
        dp[i][2] = dp[i - 2][1] + dp[i - 2][2];
    }
    return dp[n][1] + dp[n][2];
}

在上面的案例中，由于仅需多考虑前面一个状态，我们仍然可以通过扩展状态定义，使得问题重新满足无后效性。然而，某些问题具有非常严重的“有后效性”。

在这个问题中，下次跳跃依赖于过去所有的状态，因为每一次跳跃都会在更高的阶梯上设置障碍，并影响未来的跳跃。对于这类问题，动态规划往往难以解决。

实际上，许多复杂的组合优化问题（例如旅行商问题）都不满足无后效性。对于这类问题，我们通常会选择使用其他方法，例如启发式搜索、遗传算法、强化学习等，从而在有限时间内得到可用的局部最优解。